题目内容
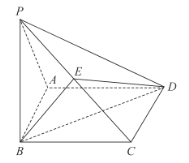
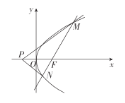
【题目】如图,在平面直角坐标系xOy中,椭圆E :![]() 的焦距为4,两条准线间的距离为8,A,B分别为椭圆E的左、右顶点.
的焦距为4,两条准线间的距离为8,A,B分别为椭圆E的左、右顶点.

(1)求椭圆E 的标准方程;
(2)已知图中四边形ABCD 是矩形,且BC=4,点M,N分别在边BC,CD上,AM与BN相交于第一象限内的点P .①若M,N分别是BC,CD的中点,证明:点P在椭圆E上;②若点P在椭圆E上,证明:![]() 为定值,并求出该定值.
为定值,并求出该定值.
【答案】(1) ![]() ;(2)①证明见解析;②证明见解析
;(2)①证明见解析;②证明见解析
【解析】
(1)由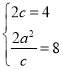 求得
求得![]() ,进而求得椭圆的方程;
,进而求得椭圆的方程;
(2)①分别求得![]() ,
,![]() 坐标,再求得直线
坐标,再求得直线![]() 与直线
与直线![]() 方程,即可求得交点坐标,进而得证;②分别设直线
方程,即可求得交点坐标,进而得证;②分别设直线![]() 的方程为
的方程为![]() ,直线
,直线![]() 的方程为
的方程为![]() ,求得点
,求得点![]() ,
,![]() 坐标,则
坐标,则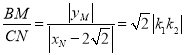 ,利用斜率公式求证即可
,利用斜率公式求证即可
(1)由题,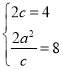 ,则
,则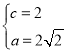 ,所以
,所以![]() ,
,
所以椭圆![]() 的标准方程为:
的标准方程为:![]()
(2)证明:①由(1)可得![]() ,
,![]() ,
,
因为![]() ,且四边形
,且四边形![]() 是矩形,
是矩形,
所以![]() ,
,![]() ,
,
因为点![]() 分别是
分别是![]() 的中点,
的中点,
所以![]() ,
,![]() ,
,
则直线![]() 为:
为:![]() ,即
,即![]() ,
,
直线![]() 为:
为:![]() ,即
,即![]() ,
,
所以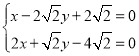 ,解得
,解得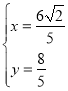 ,即
,即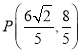
因为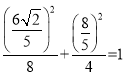 ,
,
所以点![]() 在椭圆
在椭圆![]() 上
上
②设直线![]() 的方程为
的方程为![]() ,
,
令![]() ,得
,得![]() ,
,
设直线![]() 的方程为
的方程为![]() ,
,
令![]() ,得
,得![]() ,
,
 ,
,
设![]()
![]() ,则
,则![]() ,
,
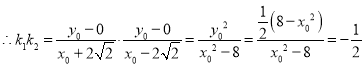 ,
,
![]()

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
【题目】北京联合张家口获得2022年第24届冬奥会举办权,我国各地掀起了发展冰雪运动的热潮,现对某高中的学生对于冰雪运动是否感兴趣进行调查,该高中男生人数是女生的1.2倍,按照分层抽样的方法,从中抽取110人,调查高中生“是否对冰雪运动感兴趣”得到如下列联表:
感兴趣 | 不感兴趣 | 合计 | |
男生 | 40 | ||
女生 | 30 | ||
合计 | 110 |
(1)补充完成上述![]() 列联表;
列联表;
(2)是否有99%的把握认为是否喜爱冰雪运动与性别有关.
附:![]() (其中
(其中![]() ).
).
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |