题目内容
(本题满分14分)如图,在四棱锥E-ABCD中,底面ABCD为正方形, AE⊥平面CDE,已知AE=3,DE=4.

(Ⅰ)若F为DE的中点,求证:BE//平面ACF;
(Ⅱ)求直线BE与平面ABCD所成角的正弦值
【答案】
解:(Ⅰ)设AC与BD相交于G,连结GF
正方形ABCD,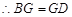 ,又
,又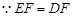 ,
,
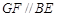 ,2分
,2分
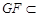 平面ACF,
平面ACF,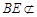 平面ACF,
平面ACF,
 平面ACF
3分
平面ACF
3分
(Ⅱ)解法一:过E点作EH⊥AD,垂足为H,连结BH1分
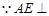 平面CDE,
平面CDE,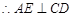 ,又
,又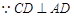 ,
,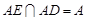 ,
,
 平面ADE,
平面ADE,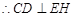 ,
,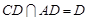 ,
,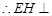 平面ABCD,
平面ABCD,
所以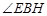 是直线BE与平面ABCD所成的角.4分
是直线BE与平面ABCD所成的角.4分
Rt 中,AE=3,DE=4,
中,AE=3,DE=4,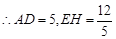 .
.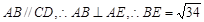 ,
,
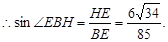 所以直线BE与平面ABCD所成角的正弦值为
所以直线BE与平面ABCD所成角的正弦值为 . 4分
. 4分
解法二: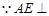 平面CDE,
平面CDE,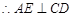 ,又
,又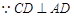 ,
,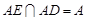 ,
,
 平面ADE,
平面ADE, 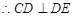 ,
,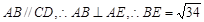 , Rt
, Rt 中,AE=3,DE=4,
中,AE=3,DE=4,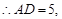
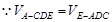 ,即
,即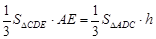 ,
,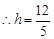
设直线BE与平面ABCD所成角为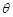 ,
,
所以直线BE与平面ABCD所成角的正弦值为 .4分
.4分
【解析】略

练习册系列答案
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案
相关题目

 、
、 的边长都是1,平面
的边长都是1,平面 平面
平面 在
在 上移动,点
上移动,点 在
在 上移动,若
上移动,若 (
( )
)
 的长;
的长; 为何值时,
为何值时, 与面
与面 所成锐二面角余弦值的大小.
所成锐二面角余弦值的大小. ,又E、F分别是C1A和C1B的中点。
,又E、F分别是C1A和C1B的中点。 (1)求证:EF//平面ABC;
(1)求证:EF//平面ABC; 平面C1CBB1;
平面C1CBB1;