题目内容
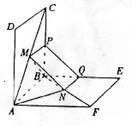
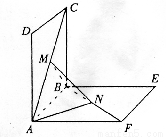
(本题满分14分)如图,正方形 、
、 的边长都是1,平面
的边长都是1,平面
 平面
平面 ,点
,点 在
在 上移动,点
上移动,点 在
在 上移动,若
上移动,若 (
( )
)

(I)求 的长;
的长;
(II) 为何值时,
为何值时, 的长最小;
的长最小;
(III)当 的长最小时,求面
的长最小时,求面 与面
与面 所成锐二面角余弦值的大小.
所成锐二面角余弦值的大小.
【答案】
又AG=BG=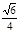 ,所以,由余弦定理有
,所以,由余弦定理有
(1) 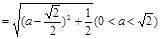
(2) 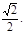
(3) 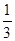
【解析】解:(Ⅰ)作MP∥AB交BC于点P,NQ∥AB交BE于点Q,连结PQ,依题意可得MP∥NQ,且MP=NQ,
 即MNQP是平行四边形,∴ MN=PQ.
即MNQP是平行四边形,∴ MN=PQ.
由已知,CM=BN=a,CB=AB=BE=1,
∴ AC=BF=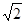 ,
,
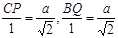
即 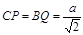
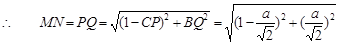
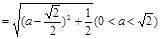 ………………4分
………………4分
(Ⅱ)由(Ⅰ),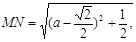 所以,当
所以,当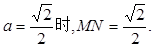
即M、N分别移动到AC、BF的中点时,MN的长最小,最小值为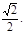 ………………9分
………………9分
(Ⅲ)取MN的中点G,连结AG、BG,
∵ AM=AN,BM=BN,G为MN的中点
∴ AG⊥MN,BG⊥MN,∠AGB即为二面角A-MN-B的平面角,
|
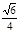 ,所以,由余弦定理有
,所以,由余弦定理有
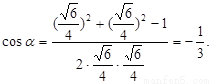
∴所求余弦值为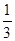 …14分
…14分

练习册系列答案
 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案
相关题目


 ,又E、F分别是C1A和C1B的中点。
,又E、F分别是C1A和C1B的中点。 (1)求证:EF//平面ABC;
(1)求证:EF//平面ABC; 平面C1CBB1;
平面C1CBB1;