Question

（本题满分14分）如图，矩形BCC1B1所在平面垂直于三角形ABC所在平面，BB1=CC1=AC=2，，又E、F分别是C1A和C1B的中点。

   （1）求证：EF//平面ABC；

   （2）求证：平面平面C1CBB1；

   （3）求异面直线AB与EB1所成的角。

 

Answer 1

【答案】

解：（Ⅰ） 在△C1AB中，∵E、F分别是C1A和C1B的中点，

       ∴EF//AB，

       ∵ABÌ平面ABC1，

       ∴EF∥平面AB        C．                     4分

       （Ⅱ） ∵平面BCC1B1⊥平面ABC，且BCC1B1为矩形

       ∴BB1⊥AB，

       又在△ABC中，AB2 + BC2= AC2 ，

       ∴AB⊥BC，∴AB⊥平面C1CBB1，

       ∴平面EFC1⊥平面C1CBB1 ．                 5分

   （Ⅲ） ∵EF∥AB, ∴∠FEB1是直线AB与EB1所成的角．           2分

       又∵ AB⊥平面C1CBB1，∴ EF⊥平面C1CBB1 ．

       在Rt△EFB1中,EF = , B1F =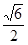, www.zxxk.com

       ∴tan∠FEB1 = =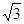, ∠FEB1 =．

       即求异面直线AB与EB1所成的角等于．                                   3分

【解析】略