题目内容
定线段AB所在的直线与定平面 相交,P为直线AB外的一点,且P不在
相交,P为直线AB外的一点,且P不在 内,若直线AP、BP与
内,若直线AP、BP与 分别交于C、D点,求证:不论P在什么位置,直线CD必过一定点.
分别交于C、D点,求证:不论P在什么位置,直线CD必过一定点.
 相交,P为直线AB外的一点,且P不在
相交,P为直线AB外的一点,且P不在 内,若直线AP、BP与
内,若直线AP、BP与 分别交于C、D点,求证:不论P在什么位置,直线CD必过一定点.
分别交于C、D点,求证:不论P在什么位置,直线CD必过一定点.证明略
设定线段AB所在直线为l,与平面 交于O点,即l∩
交于O点,即l∩ =O.
=O.
由题意可知,AP∩ =C,BP∩
=C,BP∩ =D,∴C∈
=D,∴C∈ ,D∈
,D∈ .
.
又∵AP∩BP=P,
∴AP、BP可确定一平面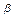 且C∈
且C∈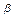 ,D∈
,D∈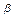 .∴CD=
.∴CD= ∩
∩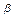 .
.
∵A∈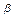 ,B∈
,B∈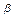 ,∴l
,∴l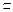
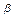 ,∴O∈
,∴O∈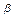 .∴O∈
.∴O∈ ∩
∩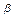 ,即O∈CD.
,即O∈CD.
∴不论P在什么位置,直线CD必过一定点.
 交于O点,即l∩
交于O点,即l∩ =O.
=O.由题意可知,AP∩
 =C,BP∩
=C,BP∩ =D,∴C∈
=D,∴C∈ ,D∈
,D∈ .
.又∵AP∩BP=P,
∴AP、BP可确定一平面
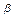 且C∈
且C∈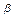 ,D∈
,D∈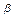 .∴CD=
.∴CD= ∩
∩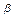 .
.∵A∈
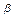 ,B∈
,B∈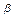 ,∴l
,∴l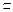
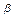 ,∴O∈
,∴O∈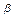 .∴O∈
.∴O∈ ∩
∩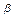 ,即O∈CD.
,即O∈CD.∴不论P在什么位置,直线CD必过一定点.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案
相关题目
 中,底面是一个矩形,
中,底面是一个矩形, ,
, ,又
,又 ,
, ,
, .
. 的大小.(用反三角函数表示)
的大小.(用反三角函数表示)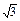 ,EF=2.
,EF=2.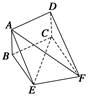
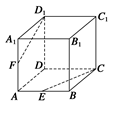
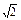 ,求点A到平面PEC的距离.
,求点A到平面PEC的距离.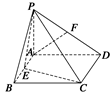

 ABCD底面是直角梯形,
ABCD底面是直角梯形, 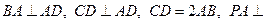 底面ABCD, E为PC的中点, PA=AD=AB=1.
底面ABCD, E为PC的中点, PA=AD=AB=1. 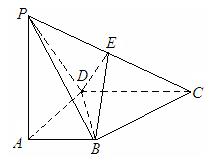
 ;
;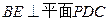 ;
; 的两条对角线的长
的两条对角线的长 ,
,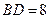 ,
, 与
与 所成的角为
所成的角为 ,
, ,
, ,
, ,
, 分别是
分别是 ,
, ,
, ,
, 的中点,求四边形
的中点,求四边形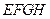 的面积
的面积