题目内容
已知函数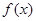 的定义域为
的定义域为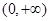 ,当
,当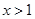 时,
时,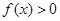 ,且对于任意的
,且对于任意的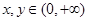 ,恒有
,恒有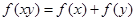 成立.
成立.
(1)求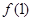 ;
;
(2)证明:函数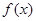 在
在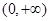 上单调递增;
上单调递增;
(3)当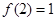 时,
时,
①解不等式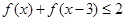 ;
;
②求函数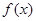 在
在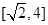 上的值域.
上的值域.
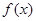 的定义域为
的定义域为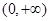 ,当
,当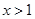 时,
时,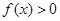 ,且对于任意的
,且对于任意的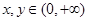 ,恒有
,恒有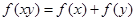 成立.
成立.(1)求
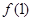 ;
;(2)证明:函数
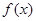 在
在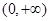 上单调递增;
上单调递增;(3)当
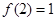 时,
时,①解不等式
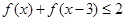 ;
;②求函数
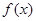 在
在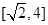 上的值域.
上的值域.(1) 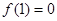 (2) 设
(2) 设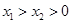 ,则
,则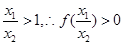 ,
,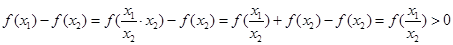 ∴函数
∴函数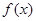 在
在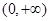 上单调递增(3) ①
上单调递增(3) ①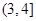 ②
②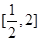
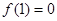 (2) 设
(2) 设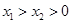 ,则
,则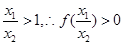 ,
,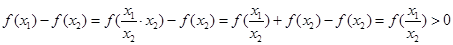 ∴函数
∴函数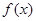 在
在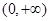 上单调递增(3) ①
上单调递增(3) ①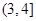 ②
②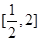
试题分析:(1)∵对于任意的
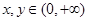 恒有
恒有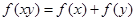 成立.
成立.∴令
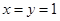 ,得:
,得: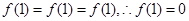 2分
2分(2)设
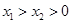 ,则
,则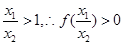 4分
4分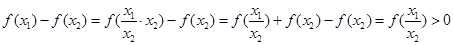
7分
∴函数
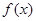 在
在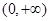 上单调递增 8分
上单调递增 8分(3)①∵对于任意的
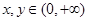 恒有
恒有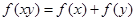 成立.
成立.∴
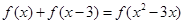
又∵
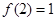 ,
,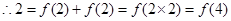
∴
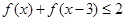 等价于
等价于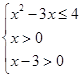 , 10分
, 10分解得:
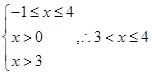 12分
12分∴所求不等式的解集为
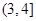
②
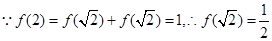
由①得:
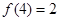
由(2)得:函数
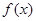 在
在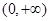 上单调递增
上单调递增故函数
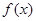 在
在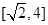 上单调递增 13分
上单调递增 13分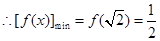 ,
, 15分
15分∴函数
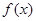 在
在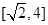 上的值域为
上的值域为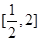 16分
16分点评:第一问抽象函数求值关键是对自变量合理赋值,第二问判定其单调性需通过定义:在
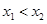 下比较
下比较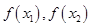 的大小关系,第三问解不等式,求函数值域都需要结合单调性将抽象函数转化为具体函数,利用单调性找到最值点的位置
的大小关系,第三问解不等式,求函数值域都需要结合单调性将抽象函数转化为具体函数,利用单调性找到最值点的位置
练习册系列答案
 优生乐园系列答案
优生乐园系列答案
相关题目
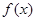 为定义在
为定义在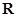 上的奇函数,当
上的奇函数,当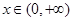 时,
时,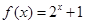 ,则当
,则当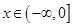 时,
时,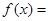 _______________.
_______________.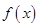 是R上的奇函数,若对于
是R上的奇函数,若对于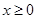 ,都有
,都有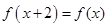 ,
, 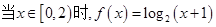 时,
时,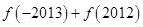 的值为
的值为 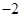
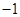

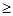 x;
x;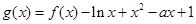 存在两个零点,求a的取值范围
存在两个零点,求a的取值范围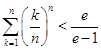
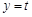 与函数
与函数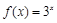 及函数
及函数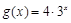 的图像分别相交于
的图像分别相交于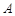 、
、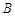 两点,则
两点,则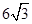 m2,为了使堤的上面与两侧面的水泥用料最省,要求断面的外周长(梯形的上底BC与两腰长的和)最小.如何设计防洪堤,才能使水泥用料最省.
m2,为了使堤的上面与两侧面的水泥用料最省,要求断面的外周长(梯形的上底BC与两腰长的和)最小.如何设计防洪堤,才能使水泥用料最省.
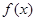 的定义域为
的定义域为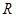 ,且满足
,且满足 为 奇函数,
为 奇函数,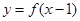 为偶函数,则下列说法中一定正确的有
为偶函数,则下列说法中一定正确的有 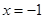 对称
对称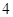
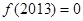
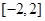 上只有一个零点
上只有一个零点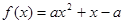
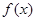 有最 大值
有最 大值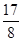 ,求实数
,求实数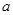 的值
的值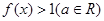
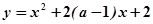 ,在
,在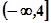 上是减少的,则
上是减少的,则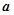 的取值范围是
的取值范围是