题目内容
已知函数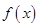 是R上的奇函数,若对于
是R上的奇函数,若对于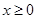 ,都有
,都有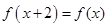 ,
, 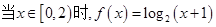 时,
时,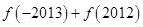 的值为
的值为
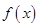 是R上的奇函数,若对于
是R上的奇函数,若对于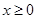 ,都有
,都有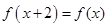 ,
, 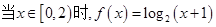 时,
时,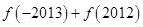 的值为
的值为 A.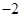 | B.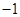 | C.1 | D.2 |
B
试题分析:根据函数的奇偶性可得f(-2013)=-f(2013),根据函数的周期性可得f(2012)=f(0),f(2013)=f(1),结合x∈[0,2)时,f(x)=log2(x+1),代入可得答案.解:∵函数f(x)是定义在R上的奇函数,∴f(-2013)=-f(2013),又∵x≥0,都有f(x+2)=f(x),,故f(2012)=f(0),f(2013)=f(1),又由当x∈[0,2)时,f(x)=log2(x+1),,∴f(2012)+f(-2013)=f(2012)-f(2013)=f(0)-f(1)=log21-log22=0-1=-1,故选C
点评:本题考查的知识点是对数函数图象与性质的综合应用,函数奇偶性的性质,其中熟练掌握函数的奇偶性和周期性是解答的关键

练习册系列答案
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案
相关题目
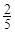 小时,种植一捆沙棘树苗用时
小时,种植一捆沙棘树苗用时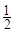 小时.应如何分配A,B两组的人数,使植树活动持续时间最短?
小时.应如何分配A,B两组的人数,使植树活动持续时间最短?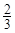 小时,于是从A组抽调6名志愿者加入B组继续种植,求植树活动所持续的时间.
小时,于是从A组抽调6名志愿者加入B组继续种植,求植树活动所持续的时间.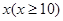 层,则每平方米的平均建筑费用为
层,则每平方米的平均建筑费用为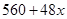 (单位:元).为了使楼房每平方米的平均综合费用最少,该楼房应建为多少层?(注:平均综合费用=平均建筑费用+平均购地费用,平均购地费用=
(单位:元).为了使楼房每平方米的平均综合费用最少,该楼房应建为多少层?(注:平均综合费用=平均建筑费用+平均购地费用,平均购地费用= )
)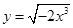 相同的是( )
相同的是( )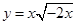
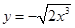
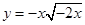
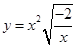
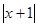 ,g(x)=2|x|+a.
,g(x)=2|x|+a.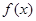 在
在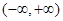 为奇函数,
为奇函数,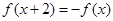 ,当
,当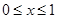 时,
时,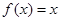 ,则
,则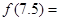 。
。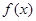 满足
满足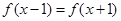 ,当
,当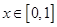 时,
时, 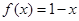 ,则关于
,则关于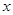 的方程
的方程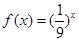 在
在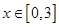 上解的个数是( )
上解的个数是( )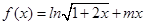 .
.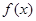 为定义域上的单调增函数,求实数
为定义域上的单调增函数,求实数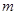 的取值范围;
的取值范围;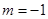 时,求函数
时,求函数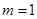 时,且
时,且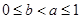 ,证明:
,证明: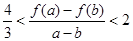 .
.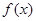 的定义域为
的定义域为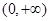 ,当
,当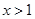 时,
时,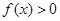 ,且对于任意的
,且对于任意的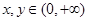 ,恒有
,恒有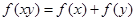 成立.
成立.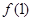 ;
;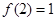 时,
时,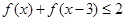 ;
;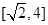 上的值域.
上的值域.