题目内容
已知函数
(1)证明:对于一切的实数x都有f(x)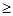 x;
x;
(2)若函数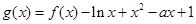 存在两个零点,求a的取值范围
存在两个零点,求a的取值范围
(3)证明: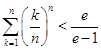

(1)证明:对于一切的实数x都有f(x)
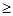 x;
x;(2)若函数
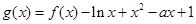 存在两个零点,求a的取值范围
存在两个零点,求a的取值范围(3)证明:
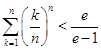
(1)构造函数,然后利用导数判断函数的单调性,再利用单调性证明,(2)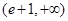
(3) 利用放缩法证明
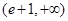
(3) 利用放缩法证明
试题分析:(1)令
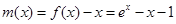
则
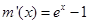 2分
2分当
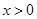 时,
时,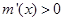 ,当
,当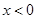 时,
时, 3分
3分故
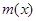 在
在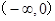 单调递减,
单调递减,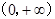 上单调递增
上单调递增所以有
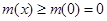 ,从而有
,从而有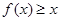 对一切实数
对一切实数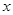 成立 4分
成立 4分(2)由
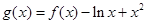 =0得
=0得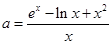 , 5分
, 5分令h(x)=
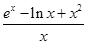 6分
6分则
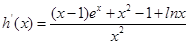 ,观察得x=1时
,观察得x=1时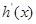 =0 7分
=0 7分当x>1时
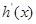 >0,当0<x<1时
>0,当0<x<1时 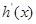 <0,
<0,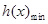 =h(1)=e+1 8分
=h(1)=e+1 8分又
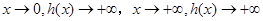
 函数
函数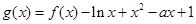 存在两个零点,则a的取值范围为
存在两个零点,则a的取值范围为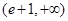 9分
9分(3) 由(1)知
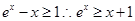 ,令
,令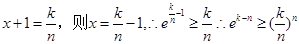 …11分
…11分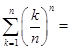
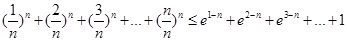
=
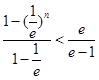 13分
13分所以
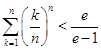 14分
14分点评:此类问题是在知识的交汇点处命题,将函数、导数、不等式、方程的知识融合在一起进行考查,重点考查了利用导数研究函数的单调性与最值等知识

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目
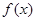 为定义在
为定义在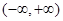 上的可导函数,且
上的可导函数,且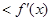 对于任意
对于任意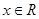 恒成立,则( )
恒成立,则( ) ,
,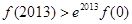
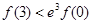 ,
,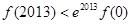
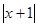 ,g(x)=2|x|+a.
,g(x)=2|x|+a.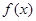 满足
满足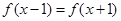 ,当
,当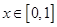 时,
时, 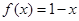 ,则关于
,则关于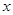 的方程
的方程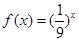 在
在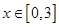 上解的个数是( )
上解的个数是( )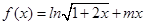 .
.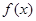 为定义域上的单调增函数,求实数
为定义域上的单调增函数,求实数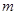 的取值范围;
的取值范围;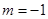 时,求函数
时,求函数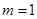 时,且
时,且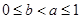 ,证明:
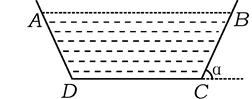
,证明: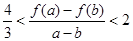 .
.
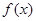 的定义域为
的定义域为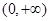 ,当
,当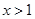 时,
时,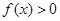 ,且对于任意的
,且对于任意的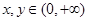 ,恒有
,恒有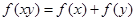 成立.
成立.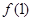 ;
;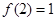 时,
时,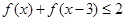 ;
;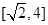 上的值域.
上的值域.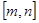 上有意义的两个函数
上有意义的两个函数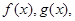 如果有任意
如果有任意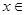
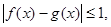 则称
则称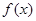 与
与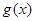 在
在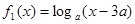 与
与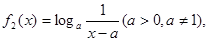 给定区间
给定区间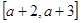 , 讨论
, 讨论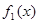 与
与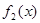 在给定区间
在给定区间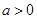 ,函数
,函数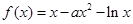 .
.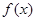 是单调函数,求实数
是单调函数,求实数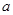 的取值范围;
的取值范围;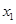 、
、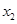 ,证明:
,证明: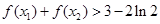 .
.