题目内容
已知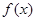 为定义在
为定义在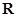 上的奇函数,当
上的奇函数,当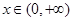 时,
时,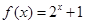 ,则当
,则当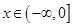 时,
时,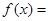 _______________.
_______________.
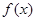 为定义在
为定义在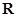 上的奇函数,当
上的奇函数,当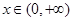 时,
时,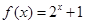 ,则当
,则当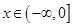 时,
时,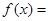 _______________.
_______________.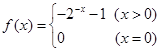
试题分析:根据题意,由于
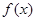 为定义在
为定义在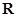 上的奇函数,当
上的奇函数,当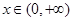 时,
时,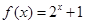 ,则当
,则当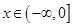 时,-
时,-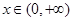 ,那么f(-x)=-f(x),
,那么f(-x)=-f(x),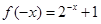 =-f(x),故可知f(x)=
=-f(x),故可知f(x)=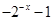 ,那么综上可知,
,那么综上可知,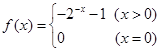
点评:解决的关键是根据函数的奇偶性以及函数的对称性来求解解析式。属于基础题。

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
题目内容
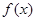 为定义在
为定义在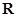 上的奇函数,当
上的奇函数,当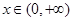 时,
时,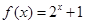 ,则当
,则当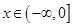 时,
时,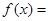 _______________.
_______________.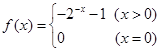
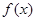 为定义在
为定义在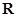 上的奇函数,当
上的奇函数,当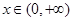 时,
时,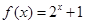 ,则当
,则当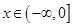 时,-
时,-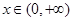 ,那么f(-x)=-f(x),
,那么f(-x)=-f(x),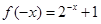 =-f(x),故可知f(x)=
=-f(x),故可知f(x)=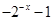 ,那么综上可知,
,那么综上可知,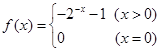

 口算能手系列答案
口算能手系列答案