题目内容
【题目】下列各组函数是同一函数的是( )
①f(x)= ![]() 与g(x)=x
与g(x)=x ![]() ;
;
②f(x)=|x|与g(x)= ![]() ;
;
③f(x)=x0与g(x)= ![]() ;
;
④f(x)=x2﹣2x﹣1与g(t)=t2﹣2t﹣1.
A.①②③
B.①③④
C.②③④
D.①②④
【答案】C
【解析】解:①f(x)= ![]() ,g(x)=x
,g(x)=x ![]() ,解析式不同,∴f(x)与g(x)不是同一函数;
,解析式不同,∴f(x)与g(x)不是同一函数;
②∵f(x)=|x|,g(x)= ![]() =|x|,故是同一函数;
=|x|,故是同一函数;
③f(x)=x0=1(x≠0), ![]() ,解析式与定义域、值域相同,故是同一函数.
,解析式与定义域、值域相同,故是同一函数.
④f(x)=x2﹣2x﹣1与g(t)=t2﹣2t﹣1对应法则和定义域相同,故是同一函数.
综上可知:②③④.
故选C.
【考点精析】掌握判断两个函数是否为同一函数是解答本题的根本,需要知道只有定义域和对应法则二者完全相同的函数才是同一函数.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
【题目】观察研究某种植物的生长速度与温度的关系,经过统计,得到生长速度(单位:毫米/月)与月平均气温的对比表如下:
温度 | -5 | 0 | 6 | 8 | 12 | 15 | 20 |
生长速度 | 2 | 4 | 5 | 6 | 7 | 8 | 10 |
(1)求生长速度![]() 关于温度
关于温度![]() 的线性回归方程;(斜率和截距均保留为三位有效数字);
的线性回归方程;(斜率和截距均保留为三位有效数字);
(2)利用(1)中的线性回归方程,分析气温从![]() 至
至![]() 时生长速度的变化情况,如果某月的平均气温是
时生长速度的变化情况,如果某月的平均气温是![]() 时,预测这月大约能生长多少.
时,预测这月大约能生长多少.
附:回归直线的斜率和截距的最小二乘法估计公式分别为:
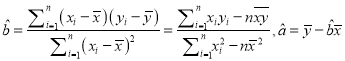 .
.