题目内容
10.在平面直角坐标系中,已知点A(1,0),点B在直线l:x=-1上运动,过点B与l垂直的直线和线段AB的垂直平分线相交于点M.(1)求动点M的轨迹E的方程;
(2)过(1)中轨迹E上的点P(1,2)作轨迹E的切线,求切线方程.
分析 (1)利用MA|=|MB|,动点M的轨迹E是以A(1,0)为焦点,直线l:x=-1为准线的抛物线,求出轨迹方程即可.
(2)设经过点P的切线方程为y-2=k(x-1),与抛物线联立利用相切,判别式为0,求解即可.
解答 解:(1)依题意,得|MA|=|MB|…(1分)
∴动点M的轨迹E是以A(1,0)为焦点,直线l:x=-1为准线的抛物线,…(3分)
∴动点M的轨迹E的方程为y2=4x.…(5分)
(2)设经过点P的切线方程为y-2=k(x-1),….(6分)
联立抛物线y2=4x消去x得:ky2-4y-4k+8=0,…(10分)
由△=16-4k(-4k+8)=0,得k=1,…(12分)
∴所求切线方程为:x-y+1=0.…(13分)
点评 本题考查轨迹方程的求法,直线与抛物线的位置关系的应用,考查计算能力.

练习册系列答案
 优生乐园系列答案
优生乐园系列答案
相关题目
20.已知中心在原点的椭圆与双曲线有公共焦点,左右焦点分别为F1,F2,且两条曲线在第一象限的交点为P,△PF1F2是以PF1为底边的等腰三角形,若|PF1|=10,椭圆与双曲线的离心率分别为e1,e2,则e2-e1的取值范围是( )
| A. | ($\frac{2}{3}$,+∞) | B. | ($\frac{4}{3}$,+∞) | C. | (0,$\frac{2}{3}$) | D. | ($\frac{2}{3}$,$\frac{4}{3}$) |
1.已知函数f(x)=(2x2-a-1)ex
(Ⅰ)若函数f(x)在[-2,2]上是单调增函数,求实数a的取值范围;
(Ⅱ)若f(x)有两个不同的极值点m,n,满足m+n≤mn+1,求f(a)的取值范围.
(Ⅰ)若函数f(x)在[-2,2]上是单调增函数,求实数a的取值范围;
(Ⅱ)若f(x)有两个不同的极值点m,n,满足m+n≤mn+1,求f(a)的取值范围.
15.直线l的倾斜角为60°,和直线l平行且经过点(-3,2)的直线方程是( )
| A. | y=$\sqrt{3}x+3\sqrt{3}$+2 | B. | y=$\frac{{\sqrt{3}}}{3}x+\sqrt{3}$+2 | C. | y=$\sqrt{3}x-3\sqrt{3}$-2 | D. | y=$\frac{{\sqrt{3}}}{3}x-\sqrt{3}$-2 |
20.在中学生综合素质评价某个维度的测评中,分“优秀、合格、尚待改进”三个等级进行学生互评.某校高一年级有男生500人,女生400人,为了了解性别对该维度测评结果的影响,采用分层抽样方法从高一年级抽取了45名学生的测评结果,并作出频数统计表如下:
表1:男生
表2:女生
(1)从表二的非优秀学生中随机选取2人交谈,求所选2人中恰有1人测评等级为合格的概率;
(2)从表二中统计数据填写下边2×2列联表,并判断是否有90%的把握认为“测评结果优秀与性别有关”.
参考数据与公式:K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$,其中n=a+b+c+d.
临界值表:
表1:男生
| 等级 | 优秀 | 合格 | 尚待改进 |
| 频数 | 15 | x | 5 |
| 等级 | 优秀 | 合格 | 尚待改进 |
| 频数 | 15 | 3 | y |
(2)从表二中统计数据填写下边2×2列联表,并判断是否有90%的把握认为“测评结果优秀与性别有关”.
| 男生 | 女生 | 总计 | |
| 优秀 | |||
| 非优秀 | |||
| 总计 |
临界值表:
| P(K2>k0) | 0.10 | 0.05 | 0.01 |
| k0 | 2.706 | 3.841 | 6.635 |
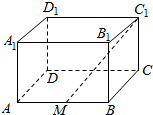 如图,长方体ABCD-A1B1C1D1中,AB=2,BC=$\sqrt{2}$,CC1=1,M为线段AB的中点.
如图,长方体ABCD-A1B1C1D1中,AB=2,BC=$\sqrt{2}$,CC1=1,M为线段AB的中点.