题目内容
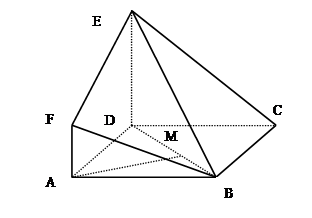
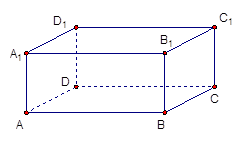
如图,在多面体ABCDE中,DB⊥平面ABC,AE∥DB,且△ABC是边长为2的等边三角形,AE=1,CD与平面ABDE所成角的正弦值为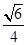 .
.
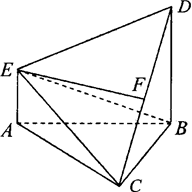
(Ⅰ)若F是线段CD的中点,证明:EF⊥面DBC;
(Ⅱ)求二面角D-EC-B的平面角的余弦值.
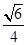 .
.
(Ⅰ)若F是线段CD的中点,证明:EF⊥面DBC;
(Ⅱ)求二面角D-EC-B的平面角的余弦值.
(Ⅰ)详见解析;(Ⅱ)二面角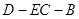 的平面角的余弦值为
的平面角的余弦值为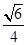 .
.
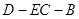 的平面角的余弦值为
的平面角的余弦值为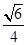 .
.试题分析:(Ⅰ)此题关键是建立空间坐标系,需要找三条两两垂直的直线,注意到△ABC是边长为2的等边三角形,可考虑取AB的中点O,则
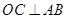 ,取BD的中点为G,则
,取BD的中点为G,则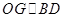 ,从而得到三条两两垂直的直线,这样就可以建立空间坐标系,根据题中条件,求出个点坐标,要证明
,从而得到三条两两垂直的直线,这样就可以建立空间坐标系,根据题中条件,求出个点坐标,要证明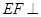 面
面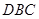 ,只需证
,只需证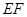 平行平面
平行平面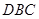 的一个法向量即可,此题也可以用传统方法来解;(Ⅱ)求二面角D-EC-B的平面角的余弦值,只需找出平面的一个法向量,利用法向量来求即可,值得注意的是,需要判断二面角是钝角还是锐角,否则求出的值不对.
的一个法向量即可,此题也可以用传统方法来解;(Ⅱ)求二面角D-EC-B的平面角的余弦值,只需找出平面的一个法向量,利用法向量来求即可,值得注意的是,需要判断二面角是钝角还是锐角,否则求出的值不对.试题解析:(Ⅰ)证明:取AB的中点O,连结OC,OD,则
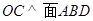 ,
,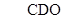 即是
即是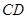 与平面
与平面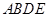 所成角,
所成角,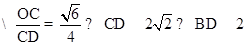 ,取BD的中点为G,以
,取BD的中点为G,以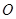 为原点,
为原点,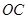 为
为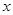 轴,
轴,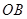 为
为 轴,
轴,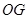 为
为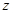 轴建立如图空间直角坐标系,则
轴建立如图空间直角坐标系,则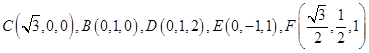 ,取BC的中点为M,则
,取BC的中点为M,则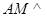 面
面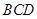
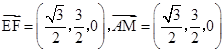 ,所以
,所以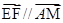 ,所以
,所以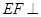 面
面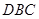 ;
;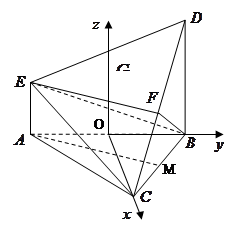
(Ⅱ)解:由上面知:
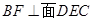 ,又
,又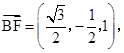 取平面DEC的一个法向量
取平面DEC的一个法向量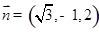 ,又
,又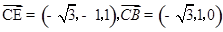 ,设平面BCE的一个法向量
,设平面BCE的一个法向量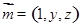 ,由
,由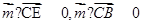 ,由此得平面BCE的一个法向量
,由此得平面BCE的一个法向量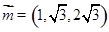 则
则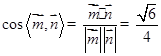 ,所以二面角
,所以二面角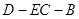 的平面角的余弦值为
的平面角的余弦值为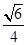 .
.
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 是边长为3的正方形,
是边长为3的正方形,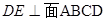 ,
, ,
,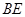 与平面
与平面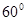 .
.
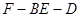 的的余弦值;
的的余弦值;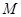 是线段
是线段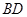 上一动点,试确定
上一动点,试确定 ,并证明你的结论.
,并证明你的结论.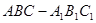 的所有棱长都为4,D为的
的所有棱长都为4,D为的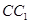 中点.
中点.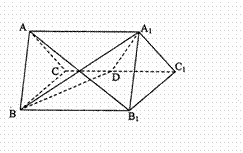
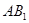 ⊥平面
⊥平面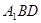 ;
;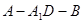 余弦值.
余弦值.
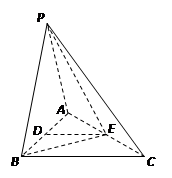
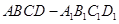 中,
中,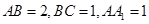
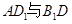 所成角;
所成角;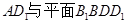 所成角的正弦.
所成角的正弦.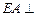 平面
平面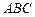 ,
,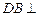 平面
平面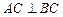 ,
,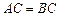
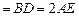 ,
,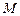 是
是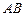 的中点.建立适当的空间直角坐标系,解决下列问题:
的中点.建立适当的空间直角坐标系,解决下列问题: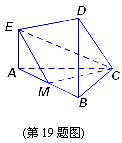
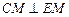 ;
;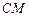 与平面
与平面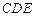 所成角的大小.
所成角的大小.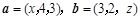 ,且
,且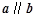 ,则
,则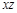 等于( )
等于( )