题目内容
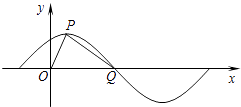
【题目】已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,0<φ< ![]() )图象如图,P是图象的最高点,Q为图象与x轴的交点,O为原点.且|OQ|=2,|OP|=
)图象如图,P是图象的最高点,Q为图象与x轴的交点,O为原点.且|OQ|=2,|OP|= ![]() ,|PQ|=
,|PQ|= ![]() .
. 
(1)求函数y=f(x)的解析式;
(2)将函数y=f(x)图象向右平移1个单位后得到函数y=g(x)的图象,当x∈[0,2]时,求函数h(x)=f(x)g(x)的最大值.
【答案】
(1)解:由余弦定理得cos∠POQ=  =
= ![]() ,
,
∴sin∠POQ= ![]() ,得P点坐标为(
,得P点坐标为( ![]() ,1),∴A=1,
,1),∴A=1, ![]() =4(2﹣
=4(2﹣ ![]() ),∴ω=
),∴ω= ![]() .
.
由f( ![]() )=sin(
)=sin( ![]() +φ)=1 可得 φ=
+φ)=1 可得 φ= ![]() ,∴y=f(x) 的解析式为 f(x)=sin(
,∴y=f(x) 的解析式为 f(x)=sin( ![]() x+
x+ ![]() ).
).
(2)解:根据函数y=Asin(ωx+)的图象变换规律求得 g(x)=sin ![]() x,…(7分)
x,…(7分)
h(x)=f(x)g(x)=sin( ![]() x+
x+ ![]() ) sin
) sin ![]() x=
x= ![]() +
+ ![]() sin
sin ![]() xcos
xcos ![]() x
x
= ![]() +
+ ![]() sin
sin ![]() =
= ![]() sin(
sin( ![]() ﹣
﹣ ![]() )+
)+ ![]() .
.
当x∈[0,2]时, ![]() ∈[﹣
∈[﹣ ![]() ,
, ![]() ],
],
∴当 ![]() ,
,
即 x=1时,hmax(x)= ![]() .
.
【解析】(1)由余弦定理得cos∠POQ 的值,可得sin∠POQ,求出P的坐标可得A的值,再由函数的周期求出ω的值,再把点P的坐标代入函数解析式求出φ,即可求得 y=f(x) 的解析式.(2)求出g(x) 的解析式,化简h(x)=f(x)g(x) 的解析式为 ![]() sin(
sin( ![]() ﹣
﹣ ![]() )+
)+ ![]() ,再根据x的范围求出h(x) 的值域,从而求得h(x) 的最大值.
,再根据x的范围求出h(x) 的值域,从而求得h(x) 的最大值.
【考点精析】本题主要考查了函数y=Asin(ωx+φ)的图象变换和三角函数的最值的相关知识点,需要掌握图象上所有点向左(右)平移![]() 个单位长度,得到函数
个单位长度,得到函数![]() 的图象;再将函数
的图象;再将函数![]() 的图象上所有点的横坐标伸长(缩短)到原来的
的图象上所有点的横坐标伸长(缩短)到原来的![]() 倍(纵坐标不变),得到函数
倍(纵坐标不变),得到函数![]() 的图象;再将函数
的图象;再将函数![]() 的图象上所有点的纵坐标伸长(缩短)到原来的
的图象上所有点的纵坐标伸长(缩短)到原来的![]() 倍(横坐标不变),得到函数
倍(横坐标不变),得到函数![]() 的图象;函数
的图象;函数![]() ,当
,当![]() 时,取得最小值为
时,取得最小值为![]() ;当
;当![]() 时,取得最大值为
时,取得最大值为![]() ,则
,则![]() ,
,![]() ,
,![]() 才能正确解答此题.
才能正确解答此题.

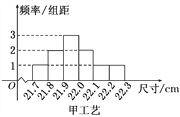
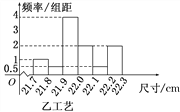
【题目】某工厂用甲、乙两种不同工艺生产一大批同一种零件,零件尺寸均在[21.7,22.3](单位:cm)之间,把零件尺寸在[21.9,22.1)的记为一等品,尺寸在[21.8,21.9)∪[22.1,22.2)的记为二等品,尺寸在[21.7,21.8)∪[22.2,22.3]的记为三等品,现从甲、乙工艺生产的零件中各随机抽取100件产品,所得零件尺寸的频率分布直方图如图所示.
P(K2≥k0) | 0.10 | 0.05 | 0.01 |
k0 | 2.706 | 3.841 | 6.635 |
附: 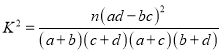
(1)根据上述数据完成下列2×2列联表,根据此数据,你认为选择不同的工艺与生产出一等品是否有关?
甲工艺 | 乙工艺 | 总计 | |
一等品 | |||
非一等品 | |||
总计 |
(2)以上述各种产品的频率作为各种产品发生的概率,若一等品、二等品、三等品的单件利润分别为30元、20元、15元,你认为以后该工厂应该选择哪种工艺生产该种零件?请说明理由.