题目内容
已知函数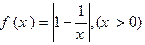
(1)当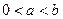 ,且
,且 时,求证:
时,求证: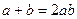
(2)是否存在实数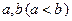 ,使得函数
,使得函数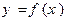 的定义域、值域都是
的定义域、值域都是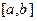 ?若存在,则求出
?若存在,则求出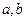 的值,若不存在,请说明理由。
的值,若不存在,请说明理由。
解:(1) ,
, ,
,
所以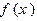 在(0,1)内递减,在(1,+
在(0,1)内递减,在(1,+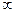 )内递增。
)内递增。
由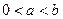 ,且
,且
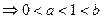 ,
,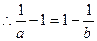 即
即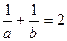 。
。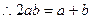
(2)不存在满足条件的实数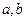 。
。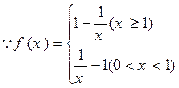
①当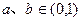 时,
时,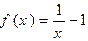 在(0,1)内递减,
在(0,1)内递减,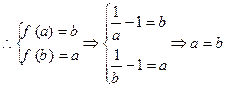 ,所以不存在。 …………………………7分
,所以不存在。 …………………………7分
②当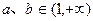 时,
时,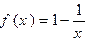 在(1,+
在(1,+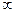 )内递增,
)内递增,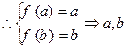 是方程
是方程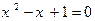 的根。
的根。
而方程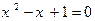 无实根。所以不存在。 …………………………10分
无实根。所以不存在。 …………………………10分
③当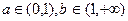 时,
时, 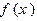 在(a,1)内递减,在(1,b)内递增,所以
在(a,1)内递减,在(1,b)内递增,所以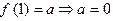 ,
,
由题意知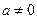 ,所以不存在。
,所以不存在。
解析

练习册系列答案
相关题目
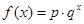 ;②
;②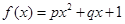 ;③
;③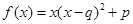 .(以上三式中、
.(以上三式中、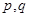 均为常数,且
均为常数,且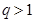 )
)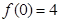 ,
,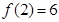 ,求出所选函数
,求出所选函数 的解析式(注:函数定义域是
的解析式(注:函数定义域是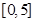 .其中
.其中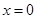 表示8月1日,
表示8月1日,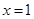 表示9月1日,…,以此类推);
表示9月1日,…,以此类推);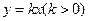 的图象与函数
的图象与函数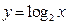 的图象交于两点
的图象交于两点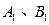 (
(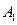 在线段
在线段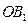 上,
上,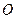 为坐标原点),过
为坐标原点),过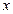 轴的垂线,垂足分别为
轴的垂线,垂足分别为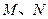 ,并且
,并且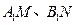 分别交函数
分别交函数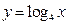 的图象于
的图象于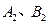 两点.
两点.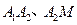 的大小关系;
的大小关系;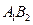 平行于
平行于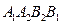 的面积.
的面积.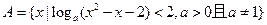 ,
,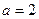 ,求集合
,求集合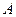 ;
; 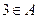 ,求实数
,求实数 的取值范围.
的取值范围.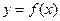 在定义域
在定义域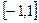 上是奇函数,又是减函数。
上是奇函数,又是减函数。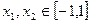 ,有
,有
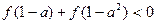 。
。 若存在x0∈R,使f(x0)=x0成立, 则称x0为f(x)的不动点. 已知函数f(x)=ax2+(b+1)x+b-1(a≠0)
若存在x0∈R,使f(x0)=x0成立, 则称x0为f(x)的不动点. 已知函数f(x)=ax2+(b+1)x+b-1(a≠0)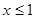 时,函数
时,函数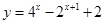 的值域为
的值域为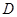 ,且当
,且当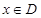 时,恒有
时,恒有 ,求实数k的取值范围.
,求实数k的取值范围.