题目内容
已知函数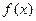
的定义域为
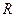,并满足(1)对于一切实数
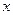，都有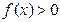
；
(2)对任意的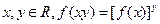
； (3)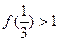
；
利用以上信息求解下列问题：
(1)求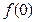
；
(2)证明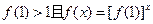
；
(3)若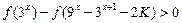
对任意的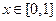
恒成立，求实数
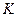的取值范围。
解析
练习册系列答案
相关题目
题目内容
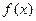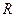已知函数的定义域为,并满足(1)对于一切实数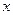，都有；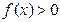
(2)对任意的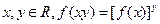； (3)；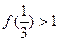
利用以上信息求解下列问题：
(1)求；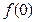
(2)证明；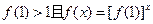
(3)若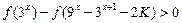对任意的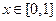恒成立，求实数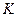的取值范围。
解析
在定义域
上是奇函数，又是减函数。
，有
。
若存在x0∈R，使f（x0）=x0成立， 则称x0为f（x）的不动点. 已知函数f（x）=ax2+（b+1）x+b－1（a≠0）
能源产品，估计能获得x∈[10,1000]万元的投资收益.现准备制定一个对科研课题组的奖励方案：奖金y（单位：万元）随投资收益x（单位：万元）的增加而增加，且奖金不超过9万元，同时奖金不超过投资收益的20%.
；(ii) y＝4lgx－3.试分析这两个函数模型
满足不等式
，求函数
的最小值．
.
（2）
的定义域为4,
的定义域为B
，求实数a的取值范围.
