Question

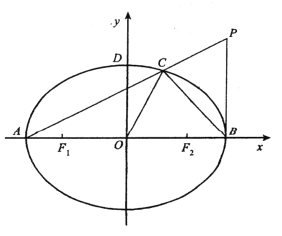
【题目】已知抛物线的焦点为，圆与轴的一个交点为，圆的圆心为，为等边三角形.

（1）求抛物线的方程

（2）设圆与抛物线交于、两点，点为抛物线上介于、两点之间的一点，设抛物线在点处的切线与圆交于、两点，在圆上是否存在点，使得直线、均为抛物线的切线，若存在求点坐标（用、表示）；若不存在，请说明理由.

Answer 1

【答案】（1）；

（2）存在圆上一点满足、均为为抛物线的切线，详见解析.

【解析】

（1）将圆的方程表示为标准方程，得出其圆心的坐标，求出点的坐标，求出抛物线的焦点的坐标，然后由为等边三角形得出为圆的半径可求出的值，进而求出抛物线的方程；

（2）设、，设切线、的方程分别为和，并写出抛物线在点的切线方程，设，并设过点的直线与抛物线相切，利用可求出、的表达式，从而可用表示直线、，然后求出点的坐标，检验点的坐标满足圆的方程，即可得出点的存在性，并得出点的坐标.

（1）圆的标准方程为，则点，抛物线的焦点为，

为等边三角形，则，即，解得，

因此，抛物线；

（2）设、.过点、作抛物线的两条切线（异于直线）交于点，并设切线，，

由替换法则，抛物线在点处的切线方程为，

即，记，①

设过点的直线与抛物线相切，

代入抛物线方程，得，

，即，，，

由①可得，，，②，同理可得，，

切线，，

联立两式消去可得，，③

代入可得，

代入②有，，

联立与圆可得，，

，

分别代入③、④可得，，

，

即切线、的交点在圆上，

故存在圆上一点，满足、均为抛物线的切线.