题目内容
【题目】某数学小组从医院和气象局获得2018年1月至6月份每月20的昼夜温差（
℃，
）和患感冒人数（
/人）的数据，画出如图的折线图.
（1）建立关于的回归方程（精确到0.01），预测2019年1月至6月份昼夜温差为41时患感冒的人数（精确到整数）；
（2）求与的相关系数，并说明与的相关性的强弱（若
，则认为与具有较强的相关性）.
参考数据：
，
，
，
.
参考公式：
相关系数
回归直线方程
，
，
.
【答案】（1）
关于
的回归方程为
，预测2019年1月至6月份昼夜温差为4℃时患感冒的人数为4人（2）相关系数
，与具有较强的相关性
【解析】
（1）由已知求得
与
的值，则线性回归方程可求，取
求得值，可预测2019年1月至6月份昼夜温差为41时患感冒的人数；
（2）求出
的值，结合的值进一步求得
值，可得与的相关性．
（1）由已知得，
，
，
关于的回归方程为，当时，
，
预测2019年1月至6月份昼夜温差为4℃时患感冒的人数为4人
（2）因为
，
，
所以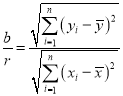
由已知得，
，
，所以
因为
，所以
，所以与具有较强的相关性.
练习册系列答案
相关题目
