题目内容
如图,AB、CD是圆的两条弦,AB与CD交于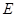 ,
, 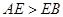 , AB是线段CD的中垂线.若AB=6,CD=
, AB是线段CD的中垂线.若AB=6,CD=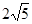 ,则线段AC的长度为 .
,则线段AC的长度为 .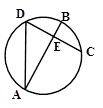
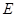 ,
, 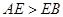 , AB是线段CD的中垂线.若AB=6,CD=
, AB是线段CD的中垂线.若AB=6,CD=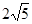 ,则线段AC的长度为 .
,则线段AC的长度为 .

试题分析:连接BC设AB,CD相交于点E,判断出AB是圆的直径.设AE=x,则EB=6-x,在直角三角形ACB中,由射影定理得CE2=AE•EB,得出关于x的方程并解出即可.解:连接BC设AB,CD相交于点E,设AE=x,∵AB是线段CD的垂直平分线,∴AB是圆的直径,∠ACB=90°…(2分)则EB=6-x,CE=
 .由射影定理得CE2=AE•EB,即有x(6-x)=5,解得x=1(舍)或x=5…∴AC2=AE•AB=5×6=30,即AC=
.由射影定理得CE2=AE•EB,即有x(6-x)=5,解得x=1(舍)或x=5…∴AC2=AE•AB=5×6=30,即AC=
点评:本题考查与圆有关的比例线段,要善于寻找有关线段的数量关系,结合相关性质、定理求解.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 与圆
与圆 交于不同的两点
交于不同的两点 若
若 ,
, 是坐标原点,那么实数
是坐标原点,那么实数 的取值范围是( )
的取值范围是( )



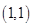 在圆
在圆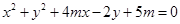 外,则实数
外,则实数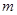 的取值范围是 。
的取值范围是 。



 ,则AC=
,则AC= 




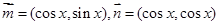 ,设函数
,设函数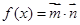
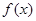 的解析式,并求最小正周期;
的解析式,并求最小正周期;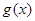 的图像是由函数
的图像是由函数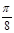 个单位得到的,求
个单位得到的,求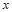 的值.
的值.  的图象上,相邻的一个最大值点与一个最小值点恰好在
的图象上,相邻的一个最大值点与一个最小值点恰好在 上,则
上,则 的最小正周期为
的最小正周期为 、
、 是单位圆
是单位圆 上的点,
上的点, 是圆与
是圆与 轴正半轴的交点,三角形
轴正半轴的交点,三角形 为正三角形, 且AB∥
为正三角形, 且AB∥
 的三个三角函数值;
的三个三角函数值; 及
及 .
.