题目内容
为保护水资源,宣传节约用水,某校4名志愿者准备去附近的甲、乙、丙三家公园进行宣传活动,每名志愿者都可以从三家公园中随机选择一家,且每人的选择相互独立.
(1)求4人恰好选择了同一家公园的概率;
(2)设选择甲公园的志愿者的人数为X,试求X的分布列.
(1)求4人恰好选择了同一家公园的概率;
(2)设选择甲公园的志愿者的人数为X,试求X的分布列.
(1)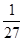 (2)X的分布列为:
(2)X的分布列为:
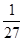 (2)X的分布列为:
(2)X的分布列为:| X | 0 | 1 | 2 | 3 | 4 |
| P | 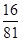 | 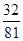 | 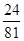 | 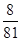 | 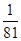 |
解:(1)设“4人恰好选择了同一家公园”为事件A.
每名志愿者都有3种选择,4名志愿者的选择共有34种等可能的情况.
事件A所包含的等可能事件的个数为3,
∴P(A)=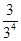 =
=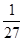 .即4人恰好选择了同一家公园的概率为
.即4人恰好选择了同一家公园的概率为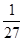 .
.
(2)设“一名志愿者选择甲公园”为事件C,则P(C)=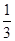 .
.
4人中选择甲公园的人数X可看作4次独立重复试验中事件C发生的次数,
因此,随机变量X服从二项分布.X可取的值为0,1,2,3,4.
P(X=i)=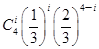 ,i=0,1,2,3,4.
,i=0,1,2,3,4.
X的分布列为:
每名志愿者都有3种选择,4名志愿者的选择共有34种等可能的情况.
事件A所包含的等可能事件的个数为3,
∴P(A)=
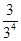 =
=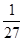 .即4人恰好选择了同一家公园的概率为
.即4人恰好选择了同一家公园的概率为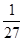 .
.(2)设“一名志愿者选择甲公园”为事件C,则P(C)=
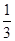 .
.4人中选择甲公园的人数X可看作4次独立重复试验中事件C发生的次数,
因此,随机变量X服从二项分布.X可取的值为0,1,2,3,4.
P(X=i)=
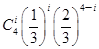 ,i=0,1,2,3,4.
,i=0,1,2,3,4.X的分布列为:
| X | 0 | 1 | 2 | 3 | 4 |
| P | 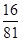 | 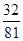 | 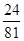 | 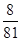 | 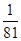 |

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 名网友的网购金额情况,得到如下数据统计表(如图):
名网友的网购金额情况,得到如下数据统计表(如图):

 千元的顾客定义为“网购达人”,网购金额不超过
千元的顾客定义为“网购达人”,网购金额不超过 .
. ,
, ,
, ,
, 的值,并补全频率分布直方图(如图(2)).
的值,并补全频率分布直方图(如图(2)). 名网友的购物体验,从“非网购达人”、“网购达人”中用分层抽样的方法确定
名网友的购物体验,从“非网购达人”、“网购达人”中用分层抽样的方法确定 人,若需从这
人,若需从这 人进行问卷调查.设
人进行问卷调查.设 为选取的
为选取的 .
. 的学生数学成绩优秀,若从班中随机找出5名学生,那么数学成绩优秀的学生数ξ~B(5,
的学生数学成绩优秀,若从班中随机找出5名学生,那么数学成绩优秀的学生数ξ~B(5,
 C.1-
C.1-