题目内容
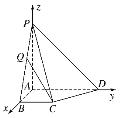
【题目】(本题满分12分)如图，在四棱锥P—ABCD中，已知PA⊥平面ABCD，且四边形ABCD为直角梯形，∠ABC＝∠BAD＝
，PA＝AD＝2，AB＝BC＝1.
(1)求点D到平面PBC的距离；
(2)设Q是线段BP上的动点，当直线CQ与DP所成的角最小时，求二面角B-CQ-D的余弦值．
【答案】（1）
.
（2）
.
【解析】分析：（1）利用等体积法即可；
（2）建立空间直角坐标系，利用换元法可得
，再结合函数
在
上的单调性，计算即得结论.
详解：(1)S△BCD=
BC×AB=, 由于PA⊥平面ABCD,从而PA即为三棱锥P-BCD的高,故VP-BCD=
S△BCD×PA=.
设点D到平面PBC的距离为h.
由PA⊥平面ABCD得PA⊥BC,又由于BC⊥AB,故BC⊥平面PAB,所以BC⊥PB.
由于BP＝
＝
,所以S△PBC=BC×PB=
.故VD-BCP=S△BCP×h=
h
因为VP-BCD=VD-BCP，所以h=
.
(2)以{
，
，
}为正交基底建立如图所示的空间直角坐标系A-xyz，则各点的坐标为B(1,0,0)，C(1,1,0)，D(0,2,0)，P(0,0,2)．
设
＝λ
，(0≤λ≤1)
因为＝(－1,0,2)，所以＝(－λ,0,2λ)，
由
＝(0,－1,0)，得
＝＋＝(－λ,－1,2λ)，
又
＝(0,－2,2)，
从而cos〈，〉＝
＝
.
设1＋2λ＝t，t∈[1,3]，
则cos2〈，〉＝
＝
≤
.
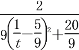当且仅当t＝
，即λ＝
时，|cos〈，〉|的最大值为
.
因为y＝cos x在
上是减函数，此时直线CQ与DP所成角取得最小值．
又因为BP＝＝，所以BQ＝BP＝.
＝(0,－1,0)，
＝(1,1，－2)
设平面PCB的一个法向量为m＝(x，y，z)，
则m·＝0，m·＝0，
即
得： y＝0，令z＝1，则x＝2.
所以m＝(2,0,1)是平面PCB的一个法向量．
又＝＋＝(－λ,－1,2λ)＝(－,－1,
)，
＝(－1,1 ,0)
设平面DCQ的一个法向量为n＝(x，y，z)，
则n·＝0，n·＝0，
即
取x＝4，则 y＝4，z＝7，
所以n＝(4,4,7)是平面DCQ的一个法向量．
从而cos〈m，n〉＝
＝
，
又由于二面角B-CQ-D为钝角，所以二面角B-CQ-D的余弦值为－.
