题目内容
【题目】设![]() 是定义在
是定义在![]() 上的函数,若存在
上的函数,若存在![]() ,使得
,使得![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减,则称
上单调递减,则称![]() 为
为![]() 上的单峰函数,
上的单峰函数,![]() 称为峰点,包含峰点的区间称为含峰区间;
称为峰点,包含峰点的区间称为含峰区间;
(1)判断下列函数:①![]() ,②
,②![]() ,哪些是“
,哪些是“![]() 上的单峰函数”?若是,指出峰点,若不是,说明理由;
上的单峰函数”?若是,指出峰点,若不是,说明理由;
(2)若函数![]() (
(![]() )是
)是![]() 上的单峰函数,求实数a的取值范围;
上的单峰函数,求实数a的取值范围;
(3)设![]() 是
是![]() 上的单峰函数,若m,
上的单峰函数,若m,![]() ),
),![]() ,且
,且![]() ,求证:
,求证:![]() 为
为![]() 的含峰区间.
的含峰区间.
【答案】(1)见解析;(2)![]() ;(3)见解析.
;(3)见解析.
【解析】
(1)依次判断各函数在![]() 上是否存在极大值点即可得出结论;
上是否存在极大值点即可得出结论;
(2)求出![]() 的极大值点,令极大值点在区间
的极大值点,令极大值点在区间![]() 上即可;
上即可;
(3)利用![]() 的单调性得出
的单调性得出![]() 的峰点在区间
的峰点在区间![]() 上即可.
上即可.
(1)①![]() ,令
,令![]() 得
得![]() ,
,
当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() ,
,
∴![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减,
上单调递减,
∴![]() 是
是![]() 上的单峰函数,峰点为
上的单峰函数,峰点为![]() ;
;
②当![]() 时,
时,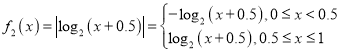 .
.
∴![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,
上单调递增,
∴![]() 不是
不是![]() 上的单峰函数;
上的单峰函数;
(2)![]() ,令
,令![]() 得
得![]() ,
,
当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() ,
,
当![]() 时,
时,![]() ,
,
∴![]() 是
是![]() 的极大值点,
的极大值点,
∵函数![]() 是
是![]() 上的单峰函数,
上的单峰函数,
∴![]() ,解得:
,解得:![]() .
.
(3)证明:∵![]() 是
是![]() 上的单峰函数,
上的单峰函数,
∴存在![]() ,使得
,使得![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减,
上单调递减,
假设![]() ,则
,则![]() 在
在![]() 上是增函数,
上是增函数,
∴![]() ,与
,与![]() 矛盾;
矛盾;
∴假设错误,故![]() ,
,
∴![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减,
上单调递减,
∴![]() 为
为![]() 的含峰区间.
的含峰区间.

练习册系列答案
相关题目