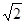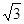题目内容
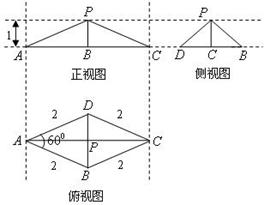
下面一组图形为三棱锥P-ABC的底面与三个侧面.已知AB⊥BC,PA⊥AB,PA⊥AC.

(1)在三棱锥P-ABC中,求证:平面ABC⊥平面PAB;
(2)在三棱锥P-ABC中,M是PA的中点,且PA=BC=3,AB=4,求三棱锥P-MBC的体积.

(1)在三棱锥P-ABC中,求证:平面ABC⊥平面PAB;
(2)在三棱锥P-ABC中,M是PA的中点,且PA=BC=3,AB=4,求三棱锥P-MBC的体积.
(1)如图,证明:∵PA⊥AB,PA⊥AC,
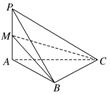
AB∩AC=A,∴PA⊥平面ABC,又∵PA?平面ABP
∴平面ABC⊥平面PAB--------------------6分
(2)∵PA=3,M是PA的中点,∴MA=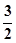 .
.
又∵AB=4,BC=3.∴VM-ABC=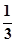 S△ABC·MA=
S△ABC·MA=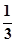 ×
×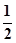 ×4×3×
×4×3×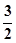 =3
=3
又VP-ABC=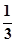 S△ABC·PA=
S△ABC·PA=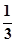 ×
×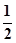 ×4×3×3=6,∴VP-MBC=VP-ABC-VM-ABC=6-3=3.
×4×3×3=6,∴VP-MBC=VP-ABC-VM-ABC=6-3=3.

AB∩AC=A,∴PA⊥平面ABC,又∵PA?平面ABP
∴平面ABC⊥平面PAB--------------------6分
(2)∵PA=3,M是PA的中点,∴MA=
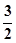 .
.又∵AB=4,BC=3.∴VM-ABC=
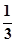 S△ABC·MA=
S△ABC·MA=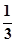 ×
×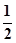 ×4×3×
×4×3×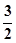 =3
=3又VP-ABC=
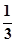 S△ABC·PA=
S△ABC·PA=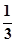 ×
×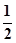 ×4×3×3=6,∴VP-MBC=VP-ABC-VM-ABC=6-3=3.
×4×3×3=6,∴VP-MBC=VP-ABC-VM-ABC=6-3=3.略

练习册系列答案
相关题目
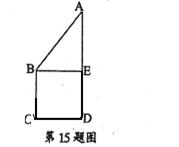
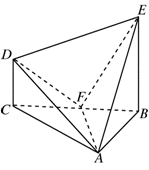
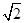 BC,将直角△ABE沿BE边折起,A点在面BCDE上的射影为D点,则翻折后的几何体中有如下描述:
BC,将直角△ABE沿BE边折起,A点在面BCDE上的射影为D点,则翻折后的几何体中有如下描述: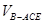 的体积是
的体积是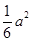 ;
;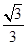 。
。
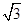 ,则异面直线AD与BC所成角的大小为 .
,则异面直线AD与BC所成角的大小为 .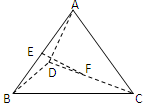
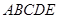 中,
中,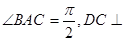 平面
平面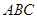 ,
,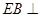 平面
平面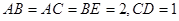 .
.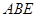 与平面
与平面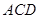 的交线为直线
的交线为直线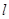 ,求证:
,求证: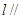 平面
平面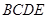 ;
;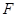 是
是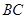 的中点,求证:平面
的中点,求证:平面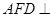 平面
平面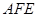 ;
;
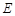 在何处时,
在何处时,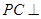 面EBD,并求出此时二面角
面EBD,并求出此时二面角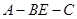 平面角的余弦值
平面角的余弦值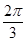
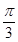
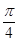
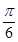

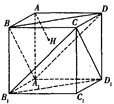
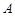 作平面
作平面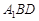 的垂线,垂足为
的垂线,垂足为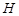 ,则以下命题中,错误的命题是
,则以下命题中,错误的命题是 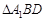 的垂心; ②
的垂心; ②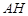 垂直平面
垂直平面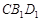 ;
;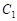 ; ④直线
; ④直线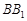 所成的角为
所成的角为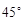
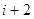 与第
与第 段所在直线必须是异面直线(其中
段所在直线必须是异面直线(其中