题目内容
1. 长方体ABCD-A1B1C1D1中,MN分别是A1B,B1D1的中点.
长方体ABCD-A1B1C1D1中,MN分别是A1B,B1D1的中点.(1)证明:MN∥平面BB1C1C;
(2)设AB=BC=2,二面角N-A1B-B1的余弦值为$\frac{\sqrt{10}}{5}$,求三棱锥M-NBC的体积.
分析 (1)取A1B1的中点G,由三角形中位线的性质证得线线平行,进一步得到线面平行,可得MN∥平面BB1C1C;
(2)求出二面角N-A1B-B1的平面角,设出AA1=2m,通过求解直角三角形得到AA1,然后求得三角形NBC的面积,再求出M到平面NBC的距离,代入三棱锥体积公式得答案.
解答 (1)证明:如图,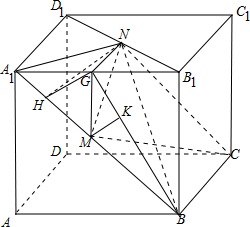 取A1B1的中点G,连接MG,NG,又M,N分别是A1B,B1D1的中点,
取A1B1的中点G,连接MG,NG,又M,N分别是A1B,B1D1的中点,
∴MG∥BB1,NG∥A1D1∥B1C1,
∴MG∥面BB1C1C,NG∥BB1C1C,
又MG∩NG=G,∴平面MNG∥平面BB1C1C,则MN∥平面BB1C1C;
(2)解:在平面A1ABB1中,过G作GH⊥A1B,垂足为H,连接NH,则∠NHG为二面角N-A1B-B1的平面角,
∴$cos∠NHG=\frac{GH}{NH}=\frac{\sqrt{10}}{5}$.
设AA1=2m,
∵AB=BC=2,∴${A}_{1}M=\sqrt{{m}^{2}+1}$,则$HG=\frac{m}{\sqrt{{m}^{2}+1}}$,
NH=$\sqrt{1+\frac{{m}^{2}}{{m}^{2}+1}}=\sqrt{\frac{2{m}^{2}+1}{{m}^{2}+1}}$,∴$\frac{m}{\sqrt{2{m}^{2}+1}}=\frac{\sqrt{10}}{5}$,解得:m=$\sqrt{2}$.
则N到BC的距离为$\sqrt{{1}^{2}+(2\sqrt{2})^{2}}=3$,
∴${S}_{△BNC}=\frac{1}{2}×2×3=3$.
过M作BG的垂线MK,则MK为M到平面NBC的距离.
∴MK=$\frac{1}{2}$×$\frac{2\sqrt{2}}{3}$=$\frac{\sqrt{2}}{3}$.
∴三棱锥M-NBC的体积V=$\frac{1}{3}×3×\frac{\sqrt{2}}{3}=\frac{\sqrt{2}}{3}$.
点评 本小题主要考查空间线面关系、二面角的度量、几何体的体积等知识,考查数形结合、化归与转化的数学思想方法,以及空间想象能力、推理论证能力和运算求解能力,是中档题.

| A. | -1 | B. | -2 | C. | 1 | D. | 2 |
| A. | y=cos6x | B. | y=-cos6x | C. | y=sin(6x+$\frac{5π}{8}$) | D. | y=sin(6x+$\frac{π}{8}$) |
 在△ABC中,AC=7,AD为∠BAC的角平分线交BC于D,且AD的长为整数,DC=4$\sqrt{2}$,cos∠DAC=$\frac{3}{5}$.
在△ABC中,AC=7,AD为∠BAC的角平分线交BC于D,且AD的长为整数,DC=4$\sqrt{2}$,cos∠DAC=$\frac{3}{5}$.