题目内容
设函数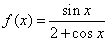 ,
,
(Ⅰ)求f(x)的单调区间;
(Ⅱ)如果对任何x≥0,都有f(x)≤ax,求a的取值范围。
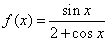 ,
,(Ⅰ)求f(x)的单调区间;
(Ⅱ)如果对任何x≥0,都有f(x)≤ax,求a的取值范围。
解:(Ⅰ)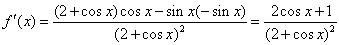 ,
,
当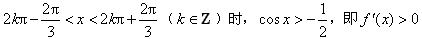 ;
;
当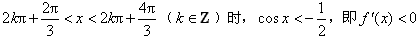 ;
;
因此f(x)在每一个区间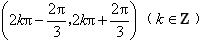 是增函数,
是增函数,
f(x)在每一个区间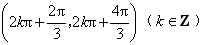 是减函数;
是减函数;
(Ⅱ)令g(x)=ax-f(x),
则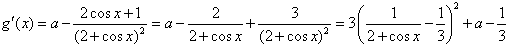 ,
,
故当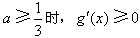 ;
;
又g(0)=0,所以当x≥0时,g(x)≥g(0)=0,
即f(x)≤ax;
当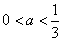 时,
时,
令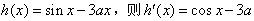 ,
,
故当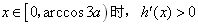 ,
,
因此h(x)在 上单调增加,
上单调增加,
故当 时,h(x)>h(0)=0,
时,h(x)>h(0)=0,
即sinx>3ax;
于是,当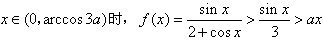 ;
;
当a≤0时,有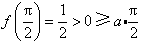 ;
;
因此,a的取值范围是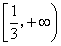 。
。
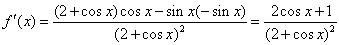 ,
,当
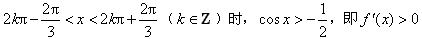 ;
;当
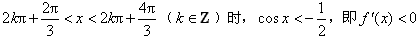 ;
;因此f(x)在每一个区间
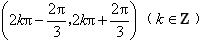 是增函数,
是增函数,f(x)在每一个区间
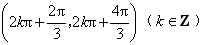 是减函数;
是减函数;(Ⅱ)令g(x)=ax-f(x),
则
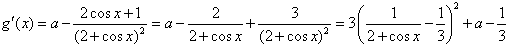 ,
,故当
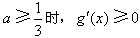 ;
;又g(0)=0,所以当x≥0时,g(x)≥g(0)=0,
即f(x)≤ax;
当
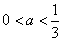 时,
时,令
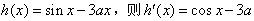 ,
,故当
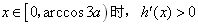 ,
,因此h(x)在
 上单调增加,
上单调增加,故当
 时,h(x)>h(0)=0,
时,h(x)>h(0)=0,即sinx>3ax;
于是,当
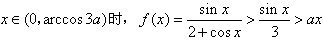 ;
;当a≤0时,有
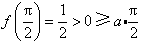 ;
;因此,a的取值范围是
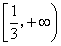 。
。
练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
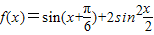 .
.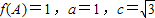 ,求b值.
,求b值.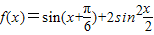 .
. ,求b值.
,求b值. .
. ,求
,求 的值.
的值. .
.
 时,求sin2x.
时,求sin2x.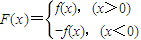 .
.