题目内容
设函数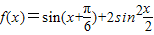 .
.(1)求f(x)的最小正周期;
(2)记△ABC的内角A,B,C的对边分别为a,b,c,若
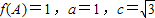 ,求b值.
,求b值.
【答案】分析:(1)把已知函数整理为y=Asin(ωx+Φ)的形式,运用公式求周期;
(2)把若f(A)=1代入整理后的函数式,求出角A的值,然后运用余弦定理或正弦定理均可求解,用正弦定理求解时注意解的情况.
解答:解:(1)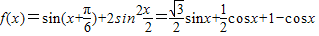 =
=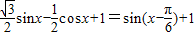 ,∴f(x)的最小正周期T=2π.
,∴f(x)的最小正周期T=2π.
(2)由f(A)=1得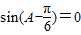 ,
,
∵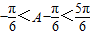 ,∴
,∴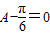 ,故A=
,故A=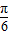 .
.
解法1:由余弦定理a2=b2+c2-2bcosA,
得b2-2b+2=0,解得b=1或2.
解法2:由正弦定理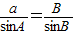 ,得
,得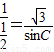 ,所以
,所以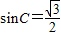 ,则
,则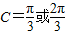 .
.
当 .
.
当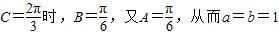 .
.
故b的值为1或2.
点评:本题考查了三角函数的周期的求法,同时考查了解三角问题,求解与三角函数有关的周期问题,往往要把解析式化为y=Asin(ωx+Φ)的形式;求解三角形,关键是给出两边及一边的对角的解的取舍.
(2)把若f(A)=1代入整理后的函数式,求出角A的值,然后运用余弦定理或正弦定理均可求解,用正弦定理求解时注意解的情况.
解答:解:(1)
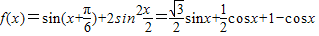 =
=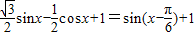 ,∴f(x)的最小正周期T=2π.
,∴f(x)的最小正周期T=2π.(2)由f(A)=1得
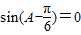 ,
,∵
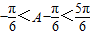 ,∴
,∴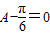 ,故A=
,故A=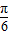 .
.解法1:由余弦定理a2=b2+c2-2bcosA,
得b2-2b+2=0,解得b=1或2.
解法2:由正弦定理
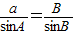 ,得
,得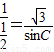 ,所以
,所以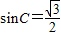 ,则
,则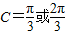 .
.当
 .
.当
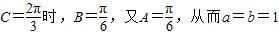 .
.故b的值为1或2.
点评:本题考查了三角函数的周期的求法,同时考查了解三角问题,求解与三角函数有关的周期问题,往往要把解析式化为y=Asin(ωx+Φ)的形式;求解三角形,关键是给出两边及一边的对角的解的取舍.

练习册系列答案
 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案
相关题目
 .
. ,求
,求 的值.
的值. .
. ,求
,求 的值.
的值. .
.
 时,求sin2x.
时,求sin2x. .
. ,c=3,求a的值.
,c=3,求a的值.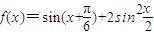 .
. ,求b值.
,求b值.