题目内容
【题目】如图，直三棱柱ABC﹣A′B′C′，∠BAC＝90°，AB＝AC＝λAA′，点M，N分别为A′B和B′C′的中点．
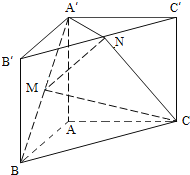
（1）证明：MN∥平面A′ACC′；
（2）若二面角A′﹣MN﹣C为直二面角，求λ的值．
【答案】（1）见解析（2）λ
．
【解析】
（1）法一：连接AB′、AC′，根据M为AB′中点，N为B′C′的中点，在
中可知MN∥AC′，又MN平面A′ACC′，所以MN∥平面A′ACC′；法二：取A′B′的中点P，连接MP、NP，根据两条相交中位线易证明平面MPN∥平面A′ACC′，从而MN∥平面A′ACC′；
（2）以A为坐标原点，分别以直线AB、AC、AA′为x，y，z轴，建立直角坐标系，写出点的坐标即可求解.
（1）证明：法一：连接AB′、AC′，
由已知∠BAC＝90°，AB＝AC，
三棱柱ABC﹣A′B′C′为直三棱柱，
所以M为AB′中点，
又因为N为B′C′的中点，
所以MN∥AC′，
又MN平面A′ACC′，
平面
，
因此MN∥平面A′ACC′；
法二：取A′B′的中点P，连接MP、NP，
M、N分别为A′B、B′C′的中点，
所以MP∥AA′，
平面，
平面，所以MP∥平面A′ACC′，
同理可得PN∥平面A′ACC′，
又MP∩NP＝P，因此平面MPN∥平面A′ACC′，
而MN平面MPN，因此MN∥平面A′ACC′．
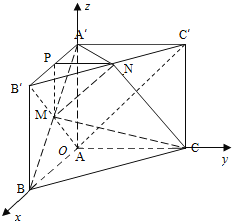
（2）以A为坐标原点，分别以直线AB、AC、AA′为x，y，z轴，建立直角坐标系，如图，
设AA′＝1，则AB＝AC＝λ，于是A（0，0，0），B（λ，0，0），C（0，λ，0），A′（0，0，1），B′（λ，0，1），C′（0，λ，1）．
所以M（
），N（
），
设
（x1，y1，z1）是平面A′MN的法向量，
，
，
由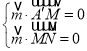
，得
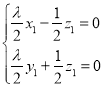，可取
，
设
（x2，y2，z2）是平面MNC的法向量，
，
由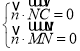
，得
，可取
，
因为二面角A'﹣MN﹣C为直二面角，
所以
，即﹣3+（﹣1）×（﹣1）+λ2＝0，解得λ
．
