题目内容
【题目】已知函数
，其中
.
（1）求函数
的单调区间；
（2）使不等式
对任意
，
恒成立时最大的
记为
，求当
时，
的取值范围.
【答案】（1）
在
上单调递增，在
单调递减（2）
（3）
【解析】
（1）求出函数的导函数，通过讨论
的范围，求出函数的单调区间即可；
（2）分离变量
得不等式，由恒成立把
，
放缩程一个新不等式，再构造一个新函数，讨论出
的范围，即可得到结论.
（1）因
的定义域为
，
，
当
时，
，∴在上单调递减；
当
时，
在上单调递减，
，
∴在
上单调递增，在
单调递减；
（2）
.
∵，，∴
，
令
，
由（1）
在
上递增；
（1）当
，即
时，
，∴
在
上递增；
∴
.
（2）当
，即
时，
，∴在上递减；
∴
.
（3）当
时，
在上递增；
存在唯一实数
，使得
，
则当
时
.当
时
.
∴
.
∴
.此时
.
令
在上递增，
，∴
.
综上所述，
.
天天向上口算本系列答案
【题目】河北省高考综合改革从2018年秋季入学的高一年级学生开始实施，新高考将实行“3+1+2”模式，其中3表示语文、数学、外语三科必选，1表示从物理、历史两科中选择一科，2表示从化学、生物、政治、地理四科中选择两科.某校2018级入学的高一学生选科情况如下表：
选科组合 | 物化生 | 物化政 | 物化地 | 物生政 | 物生地 | 物政地 | 史政地 | 史政化 | 史生政 | 史地化 | 史地生 | 史化生 | 合计 |
男 | 130 | 45 | 55 | 30 | 25 | 15 | 30 | 10 | 40 | 10 | 15 | 20 | 425 |
女 | 100 | 45 | 50 | 35 | 35 | 35 | 40 | 20 | 55 | 15 | 25 | 20 | 475 |
合计 | 230 | 90 | 105 | 65 | 60 | 50 | 70 | 30 | 95 | 25 | 40 | 40 | 900 |
（1）完成下面的
列联表，并判断是否在犯错误概率不超过0.01的前提下，认为“选择物理与学生的性别有关”？
（2）以频率估计概率，从该校2018级高一学生中随机抽取3名同学，设这三名同学中选择物理的人数为
，求的分布列和数学期望.
选择物理 | 不选择物理 | 合计 | |
男 | 425 | ||
女 | 475 | ||
合计 | 900 |
附表及公式：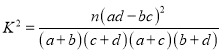
| 0.150 | 0.100 | 0.050 | 0.010 |
| 2.072 | 2.706 | 3.841 | 6.635 |
