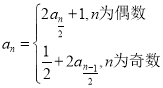题目内容
【题目】若数列![]() 对任意的
对任意的![]() ,都有
,都有![]()
![]() ,且
,且![]() ,则称数列
,则称数列![]() 为“k级创新数列”.
为“k级创新数列”.
(1)已知数列![]() 满足
满足![]() 且
且![]() ,试判断数列
,试判断数列![]() 是否为“2级创新数列”,并说明理由;
是否为“2级创新数列”,并说明理由;
(2)已知正数数列![]() 为“k级创新数列”且
为“k级创新数列”且![]() ,若
,若![]() ,求数列
,求数列![]() 的前n项积
的前n项积![]() ;
;
(3)设![]() ,
,![]() 是方程
是方程![]() 的两个实根
的两个实根![]() ,令
,令![]() ,在(2)的条件下,记数列
,在(2)的条件下,记数列![]() 的通项
的通项![]() ,求证:
,求证:![]()
![]() .
.
【答案】(1)数列![]() 是“2级创新数列”,见解析(2)
是“2级创新数列”,见解析(2)![]() (3)见解析
(3)见解析
【解析】
(1)数列![]() 是“2级创新数列”,下面给出证明:
是“2级创新数列”,下面给出证明:![]() ,可得
,可得
![]()
![]()
![]() ,即可证明.
,即可证明.
(2)正数数列![]() 为“k级创新数列”且
为“k级创新数列”且![]() ,
,![]() .又
.又![]() ,
,
利用指数的运算性质可得数列![]() 的前n项积
的前n项积![]() .
.
(3)![]() ,
,![]() 是方程
是方程![]() 的两个实根
的两个实根![]() ,可得
,可得![]()
![]() .在(2)的条件下,记数列
.在(2)的条件下,记数列![]() 的通项
的通项![]()
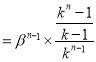
![]() .
.
(1)解:数列![]() 是“2级创新数列”,下面给出证明:
是“2级创新数列”,下面给出证明:
![]() ,
,
![]()
![]()
![]() ,
,
![]() 数列
数列![]() 是“2级创新数列”.
是“2级创新数列”.
(2)解:![]() 正数数列
正数数列![]() 为“k级创新数列”且
为“k级创新数列”且![]() ,
,
![]() .
.
![]() .
.
又![]() ,
,
![]() 数列
数列![]() 的前n项积
的前n项积
![]()
![]()
![]() .
.
(3)证明:![]() ,
,![]() 是方程
是方程![]() 的两个实根
的两个实根![]() ,
,
![]()
![]() .
.
在(2)的条件下,记数列![]() 的通项
的通项
![]()
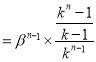
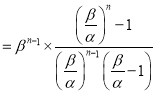
![]() .
.
![]() .
.
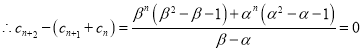 .
.
![]() .
.

练习册系列答案
相关题目