Question

【题目】设函数f（x）=ax2﹣（a+1）x+1．
（1）若不等式f（x）＜mx的解集为{x|1＜x＜2}，求实数a、m的值；
（2）解不等式f（x）＜0．

Answer 1

【答案】
（1）解：∵f（x）=ax2﹣（a+1）x+1，

∴不等式f（x）＜mx等价于ax2﹣（a+m+1）x+1＜0，

依题意知不等式ax2﹣（a+m+1）x+1＜0的解集为{x|1＜x＜2}，

∴a＞0且1和2为方程ax2﹣（a+m+1）x+1=0的两根，

∴ ，

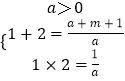解得 ，

∴实数a、m的值分别为a=1、m=0

（2）解：不等式f（x）＜0可化为（ax﹣1）（x﹣1）＜0，

（ⅰ）当a=0时，不等式f（x）＜0等价于﹣x+1＜0，解得x＞1，

故原不等式的解集为{x|x＞1}，

（ⅱ）当a＞0时，不等式f（x）＜0等价于 ，

①当0＜a＜1时 ，不等式 的解集为 ，

即原不等式的解集为 ，

②当a=1时，不等式 的解集为φ，

即原不等式的解集为φ，

③当a＞1时 ，不等式 的解集为 ，

即原不等式的解集为 ，

（ⅲ）当a＜0时，不等式f（x）＜0等价于 ，

∵a＜0，

∴ ，

∴不等式 的解集为{x|x＜ 或x＞1}，

即原不等式的解集为{x|x＜ 或x＞1}，

综上所述，当a＞1时不等式f（x）＜0的解集为 ，

当a=1时不等式f（x）＜0的解集为φ，

当0＜a＜1时不等式f（x）＜0的解集为 ，

当a=0时不等式f（x）＜0的解集为{x|x＞1}，

当a＜0时不等式f（x）＜0的解集为为{x|x＜ 或x＞1}

【解析】（1）根据一元二次不等式的解集，利用根与系数的关系，即可求出实数a、m的值；（2）不等式化为（ax﹣1）（x﹣1）＜0，讨论a=0和a＞0、a＜0时，求出不等式f（x）＜0的解集即可．
【考点精析】解答此题的关键在于理解二次函数的性质的相关知识，掌握当时，抛物线开口向上，函数在上递减，在上递增；当时，抛物线开口向下，函数在上递增，在上递减，以及对解一元二次不等式的理解，了解求一元二次不等式解集的步骤：一化：化二次项前的系数为正数;二判：判断对应方程的根;三求：求对应方程的根;四画：画出对应函数的图象;五解集：根据图象写出不等式的解集;规律：当二次项系数为正时，小于取中间，大于取两边．