题目内容
8.已知△ABC的三边分别为a,b,c,且其中任意两边长均不相等,若1a1a,1b1b,1c1c成等差数列.(1)比较√ba√ba与√cb√cb的大小,并证明你的结论;
(2)求证:角B不可能是钝角.
分析 (1)由1a1a,1b1b,1c1c成等差数列,利用等差数列的性质列出关系式,整理即可得到结果;
(2)由等差数列的性质列出关系式,表示出b,再利用余弦定理表示出cosB,把表示出的b代入并利用基本不等式判断cosB的正负,即可做出判断.
解答 解:(1)∵a,b,c任意两边长均不相等,若1a1a,1b1b,1c1c成等差数列,
∴2b2b=1a1a+1c1c>2√ac2√ac,即1b1b>1√ac1√ac,
则√cb√cb>√ba√ba;
(2)∵2b2b=1a1a+1c1c,
∴b=2aca+c2aca+c,
由余弦定理得:cosB=a2+c2−b22aca2+c2−b22ac=a2+c2−(2aca+c)22ac=(a2+c2)(a+c)2−4a2c22ac(a+c)2≥2ac•4ac−4a2c22ac(a+c)2=4ac−2ac(a+c)2=2ac(a+c)2>0,
则B不可能为钝角.
点评 此题考查了余弦定理,以及数列的应用,熟练掌握余弦定理是解本题的关键.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目
3.函数f(x)=log2(1-3x)的定义域是( )
| A. | (0,+∞) | B. | [0,+∞) | C. | (-∞,0) | D. | (-∞,0] |

 如图,在四棱锥P-ABCD中,底面ABCD是直角梯形,∠ABC=∠BCD=90°,面PAD⊥面ABCD,PA=PD=CD=BC=1,AB=2,AD=
如图,在四棱锥P-ABCD中,底面ABCD是直角梯形,∠ABC=∠BCD=90°,面PAD⊥面ABCD,PA=PD=CD=BC=1,AB=2,AD=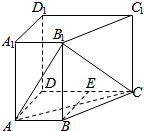 如图,在四棱锥ABCD-A1B1C1D中,侧棱AA1⊥底面ABCD,AB∥DC,AA1=1,AB=3k,AD=4k,BC=5k,DC=6k(k>0),现将与四棱锥ABCD-A1B1C1D形状和大小完全相同的两个四棱柱拼接成一个新的棱柱,规定:若拼接成的新的四棱锥形状和大小完全相同,则视为同一种拼接方案.问:共有几种不同的方案?在这些拼接成的新的四棱柱中,记其中最小的表面积为f(k),写出f(k)的表达式.
如图,在四棱锥ABCD-A1B1C1D中,侧棱AA1⊥底面ABCD,AB∥DC,AA1=1,AB=3k,AD=4k,BC=5k,DC=6k(k>0),现将与四棱锥ABCD-A1B1C1D形状和大小完全相同的两个四棱柱拼接成一个新的棱柱,规定:若拼接成的新的四棱锥形状和大小完全相同,则视为同一种拼接方案.问:共有几种不同的方案?在这些拼接成的新的四棱柱中,记其中最小的表面积为f(k),写出f(k)的表达式.