题目内容
16. 如图,在四棱锥P-ABCD中,底面ABCD是直角梯形,∠ABC=∠BCD=90°,面PAD⊥面ABCD,PA=PD=CD=BC=1,AB=2,AD=$\sqrt{2}$.
如图,在四棱锥P-ABCD中,底面ABCD是直角梯形,∠ABC=∠BCD=90°,面PAD⊥面ABCD,PA=PD=CD=BC=1,AB=2,AD=$\sqrt{2}$.(1)证明:AP⊥面PBD.
(2)若点E是线段PB上一点,且$\overrightarrow{PE}$=2$\overrightarrow{EB}$,求三棱锥P-ADE的体积.
分析 (1)利用勾股定理证明BD⊥AD,AP⊥PD,根据线面垂直的判定定理,证明AP⊥面PBD.
(2)转换底面,即可求三棱锥P-ADE的体积.
解答 (1)证明:在直角梯形ABCD中,∠ABC=∠BCD=90°,CD=BC=1,AB=2,AD=$\sqrt{2}$.
∴AD2+BD2=AB2,
∴BD⊥AD,
∵面PAD⊥面ABCD,面PAD∩面ABCD=AD,
∴BD⊥面PAD,
∴BD⊥AP,
∵PA=PD=1,AD=$\sqrt{2}$,
∴PA2+PD2=AD2,
∴AP⊥PD,
∵BD∩PD=D,
∴AP⊥面PBD.
(2)解:由(1)BD⊥面PAD,
∵$\overrightarrow{PE}$=2$\overrightarrow{EB}$,
∴E到平面PAD的距离=$\frac{2}{3}$BD=$\frac{2\sqrt{2}}{3}$,
∴三棱锥P-ADE的体积=三棱锥E-PAD的体积=$\frac{1}{3}×\frac{1}{2}×1×1×\frac{2\sqrt{2}}{3}$=$\frac{\sqrt{2}}{9}$.
点评 本题考查线面垂直的判定定理,考查三棱锥P-ADE的体积,正确运用线面垂直的判定定理是关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
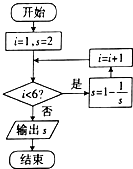
 如图,经过圆锥顶点S的一个截面SAB和底面成60°的二面角,截底面所得弧长所对圆心角为120°,底面圆心O到截面SAB的距离为30cm,求棱锥S-OAB的体积.
如图,经过圆锥顶点S的一个截面SAB和底面成60°的二面角,截底面所得弧长所对圆心角为120°,底面圆心O到截面SAB的距离为30cm,求棱锥S-OAB的体积.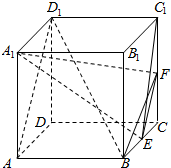 已知四棱柱ABCD-A1B1C1D1的底面是边长为2的正方形且AA1⊥底面ABCD,AA1=4,E为BC的中点,F为CC1的中点.
已知四棱柱ABCD-A1B1C1D1的底面是边长为2的正方形且AA1⊥底面ABCD,AA1=4,E为BC的中点,F为CC1的中点.