题目内容
【题目】设集合A=[0， 
），B=[ ，1]，函数f （x）=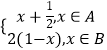 
，若x0∈A，且f[f （x0）]∈A，则x0的取值范围是（ ）
A.（0， 
]
B.[ ， ]
C.（ ， ）
D.[0， 
]
【答案】C
【解析】解：∵0≤x0＜ 
，∴f（x0）=x0 + ∈[ ，1]B，
∴f[f（x0）]=2（1﹣f（x0））=2[1﹣（x0+ ）]=2（ ﹣x0）．
∵f[f（x0）]∈A，∴0≤2（ ﹣x0）＜ ，∴ 
＜x0≤ ．
又∵0≤x0＜ ，∴ ＜x0＜ ．
故选C．
【考点精析】根据题目的已知条件，利用元素与集合关系的判断和函数的值的相关知识可以得到问题的答案，需要掌握对象
与集合
的关系是
，或者
，两者必居其一；函数值的求法：①配方法(二次或四次)；②“判别式法”；③反函数法；④换元法；⑤不等式法；⑥函数的单调性法．
七彩题卡口算应用一点通系列答案【题目】某公司为确定下一年度投入某种产品的宣传费，需了解年宣传费
（单位：万元）对年销售量
（单位：吨）和年利润
（单位：万元）的影响。对近六年的年宣传费
和年销售量
的数据作了初步统计，得到如下数据：
年份 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 |
年宣传费 | 38 | 48 | 58 | 68 | 78 | 88 |
年销售量 | 16.8 | 18.8 | 20.7 | 22.4 | 24.0 | 25.5 |
经电脑拟，发现年宣传费（万元）与年销售量（吨）之间近似满足关系式
即
。对上述数据作了初步处理，得到相关的值如下表：
|
|
|
|
75.3 | 24.6 | 18.3 | 101.4 |
（1）根据所给数据，求关于的回归方程；
（2）规定当产品的年销售量（吨）与年宣传费（万元）的比值在区间
内时认为该年效益良好。现从这6年中任选2年，记其中选到效益良好年的数量为
，试求随机变量的分布列和期望。（其中
为自然对数的底数， 
）
附：对于一组数据
，其回归直线
中的斜率和截距的最小二乘估计分别为
【题目】某城市理论预测2010年到2014年人口总数与年份的关系如下表所示
年份2010+x（年） | 0 | 1 | 2 | 3 | 4 |
人口数y（十万） | 5 | 7 | 8 | 11 | 19 |
(1)请根据上表提供的数据，求出y关于x的线性回归方程；
(2) 据此估计2015年该城市人口总数。
