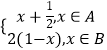题目内容
【题目】已知函数f(x)的定义域为{x|x∈R，且x≠0}，对定义域内的任意x1、x2，都有f(x1·x2)＝f(x1)＋f(x2)，且当x>1时，f(x)>0.
(1)求证：f(x)是偶函数；
(2)求证：f(x)在(0，＋∞)上是增函数．
【答案】（1）见解析 （2）见解析
【解析】证明： (1)因对定义域内的任意x1、x2都有
f(x1·x2)＝f(x1)＋f(x2)，
令x1＝x，x2＝－1，
则有f(－x)＝f(x)＋f(－1)．
又令x1＝x2＝－1，得2f(－1)＝f(1)．
再令x1＝x2＝1，得f(1)＝0，
从而f(－1)＝0，
于是有f(－x)＝f(x)，所以f(x)是偶函数．
(2)设0<x1<x2，
则f(x1)－f(x2)＝f(x1)－f(x1·
)＝f(x1)－[f(x1)＋f(
)]＝－f(
)，
由于0<x1<x2，所以
>1，从而f(
)>0，
故f(x1)－f(x2)<0，即f(x1)<f(x2)，
所以f(x)在(0，＋∞)上是增函数．
练习册系列答案
学练快车道口算心算速算天天练系列答案
相关题目
