题目内容
已知函数 ,
, ,
, .
.
(1)当 时,求函数
时,求函数 的最小值;
的最小值;
(2)若函数 的最小值为
的最小值为 ,令
,令 ,求
,求 的取值范围.
的取值范围.
(1) ;(2)
;(2) .
.
解析试题分析:(1)取绝对值,化简,配方法求最小值;(2)取绝对值,然后对 的范围经行分类讨论(注意以两二次函数的对称轴为界进行分类),最后求出最小值表达式,利用图象(配方法、函数性质法也可以)求最值。
的范围经行分类讨论(注意以两二次函数的对称轴为界进行分类),最后求出最小值表达式,利用图象(配方法、函数性质法也可以)求最值。
试题解析:(Ⅰ) =
= ,
,
由 ,可知
,可知 ;
;
由 ,可知
,可知 。
。
所以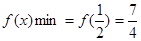 。 5分
。 5分
(Ⅱ)
1)当 ,
, ; 7分
; 7分
2)当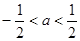 ,
, ; 9分
; 9分
3)当 ,
, ; 11分
; 11分
所以 ,
, 图解得:
图解得: 。 15分
。 15分
考点:(1)分段函数最值问题;(2)含参数分段函数讨论

练习册系列答案
 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目
 表示自然数
表示自然数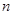 的所有因数中最大的那个奇数,例如:9的因数有1,3,9,
的所有因数中最大的那个奇数,例如:9的因数有1,3,9, ,10的因数有1,2,5,10,
,10的因数有1,2,5,10, ,那么
,那么
 ;
; .
.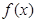 满足条件
满足条件 ,及
,及 .
. 上的最值.
上的最值. .
.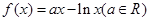 。
。 时,求曲线
时,求曲线 在
在 处切线的斜率;
处切线的斜率; 的单调区间;
的单调区间; 时,求
时,求 上的最小值。
上的最小值。 在其定义域上为奇函数.
在其定义域上为奇函数.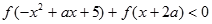 对任意实数
对任意实数 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围. 的图象为C1,C1关于点A(2,1)对称的图象为C2,C2对应的函数为g(x).
的图象为C1,C1关于点A(2,1)对称的图象为C2,C2对应的函数为g(x). 的部分对应值如下表:
的部分对应值如下表: 的解集是 。
的解集是 。  是奇函数,则
是奇函数,则 .w.w.w.k.s.5.u.c.o.m
.w.w.w.k.s.5.u.c.o.m 
