题目内容
14．在△ABC中，若$\overrightarrow{AB}$•$\overrightarrow{BC}$=$\overrightarrow{BC}$•$\overrightarrow{CA}$=$\overrightarrow{CA}$•$\overrightarrow{AB}$，则该三角形是（ ）| A． | 等腰三角形 | B． | 直角三角形 | C． | 等腰直角三角形 | D． | 等边三角形 |
分析 设AC的中点为D，由$\overrightarrow{BC}$•$\overrightarrow{CA}$=$\overrightarrow{CA}$•$\overrightarrow{AB}$可得$\overrightarrow{CA}（\overrightarrow{BC}-\overrightarrow{CA}）=0$，$\overrightarrow{BD}⊥\overrightarrow{AC}$且BD平分AC．BA=BC，同理可证：CA=CB．即可得出．
解答 解：设AC的中点为D，
$\overrightarrow{BC}$•$\overrightarrow{CA}$=$\overrightarrow{CA}$•$\overrightarrow{AB}$可得$\overrightarrow{CA}（\overrightarrow{BC}-\overrightarrow{CA}）=0$，$\overrightarrow{BD}⊥\overrightarrow{AC}$且BD平分AC．
∴BA=BC，同理可证：CA=CB．
∴BA=BC=AC．
∴△ABC是等边三角形．
故选：D．
点评 本题考查了向量的平行四边形法则、向量垂直与数量积的关系、等腰三角形与等边三角形的判定与性质，考查了推理能力，属于基础题．
练习册系列答案
相关题目
4．
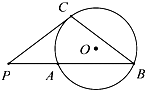如图，PC是⊙O的切线，C为切点，PAB为割线，PC=2，PA=1，∠P=60°，则BC=（ ）
如图，PC是⊙O的切线，C为切点，PAB为割线，PC=2，PA=1，∠P=60°，则BC=（ ）| A． | 3 | B． | 2 | C． | 3$\sqrt{2}$ | D． | 2$\sqrt{3}$ |
9．若实数x，y满足$\left\{\begin{array}{l}{x-4y+3≤0}\\{3x+5y-25≤0}\\{x≥1}\end{array}\right.$，则函数z=2x+y的最大值为（ ）
| A． | 12 | B． | $\frac{32}{5}$ | C． | 3 | D． | 15 |
19．圆x2+y2=1在伸缩变换$\left\{\begin{array}{l}x'=2x\\ y'=3y\end{array}\right.$的作用下，所得方程是（ ）
| A． | 4x′2+9y′2=1 | B． | $\frac{{{{x'}^2}}}{2}+\frac{{{{y'}^2}}}{3}=1$ | C． | $\frac{{{{x'}^2}}}{9}+\frac{{{{y'}^2}}}{4}=1$ | D． | $\frac{{{{x'}^2}}}{4}+\frac{{{{y'}^2}}}{9}=1$ |
如图，在三棱锥A-BOC中，OA⊥底面BOC，∠OAB=∠OAC=30°，AB=AC=4，BC=2$\sqrt{2}$，动点D在线段AB上．