题目内容
【题目】已知点![]() ,点P是圆C:
,点P是圆C:![]() 上的任意一点,线段PQ的垂直平分线与直线CP交于点M.
上的任意一点,线段PQ的垂直平分线与直线CP交于点M.
![]() 求点M的轨迹方程;
求点M的轨迹方程;
![]() 过点
过点![]() 作直线与点M的轨迹交于点E,过点
作直线与点M的轨迹交于点E,过点![]() 作直线与点M的轨迹交于点
作直线与点M的轨迹交于点![]() F不重合
F不重合![]() ,且直线AE和直线BF的斜率互为相反数,直线EF的斜率是否为定值,若为定值,求出直线EF的斜率;若不是定值,请说明理由.
,且直线AE和直线BF的斜率互为相反数,直线EF的斜率是否为定值,若为定值,求出直线EF的斜率;若不是定值,请说明理由.
【答案】(1)![]() ;(2)定值
;(2)定值![]() .
.
【解析】
(1)根据中垂线的性质得出![]() ,然后计算出
,然后计算出![]() ,结合椭圆的定义得知点
,结合椭圆的定义得知点![]() 的轨迹为椭圆,可得出
的轨迹为椭圆,可得出![]() 和
和![]() 的值,进而求得
的值,进而求得![]() 的值,于是可得出点
的值,于是可得出点![]() 的轨迹方程;
的轨迹方程;
(2)设直线![]() 的方程为
的方程为![]() ,则直线
,则直线![]() 的方程为
的方程为![]() ,将直线
,将直线![]() 、
、![]() 的方程分别与曲线
的方程分别与曲线![]() 的方程联立,利用韦达定理求出的点
的方程联立,利用韦达定理求出的点![]() 的坐标,然后利用两点间的斜率公式求出直线
的坐标,然后利用两点间的斜率公式求出直线![]() 的斜率,从而证明结论.
的斜率,从而证明结论.
(1)如下图所示,

连接![]() ,则
,则![]() ,
,
又![]() ,所以点
,所以点![]() 的轨迹是以
的轨迹是以![]() 为焦点的椭圆,
为焦点的椭圆,
因为![]() ,所以
,所以![]() .
.
故点![]() 的轨迹方程是
的轨迹方程是![]() ;
;
(2)设直线![]() 的方程为
的方程为![]() ,则直线
,则直线![]() 的方程为
的方程为![]() ,
,
由![]() ,消去
,消去![]() 整理得
整理得![]() .
.
设交点![]() 、
、![]() ,
,
则![]() ,
,![]() .
.
由![]() ,消去
,消去![]() 整理得
整理得![]() ,
,
则![]() .
.
所以,![]() .
.
故直线![]() 的斜率为定值,其斜率为
的斜率为定值,其斜率为![]() .
.

练习册系列答案
相关题目
【题目】为了分析某个高三学生的学习状态.现对他前5次考试的数学成绩x,物理成绩y进行分析.下面是该生前5次考试的成绩.
数学 | 120 | 118 | 116 | 122 | 124 |
物理 | 79 | 79 | 77 | 82 | 83 |
附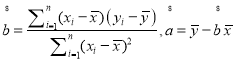 .
.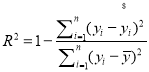 .
.
![]() 已知该生的物理成绩y与数学成绩x是线性相关的,求物理成绩y与数学成绩x的回归直线方程;
已知该生的物理成绩y与数学成绩x是线性相关的,求物理成绩y与数学成绩x的回归直线方程;
![]() 我们常用
我们常用![]() 来刻画回归的效果,其中
来刻画回归的效果,其中![]() 越接近于1,表示回归效果越好.求
越接近于1,表示回归效果越好.求![]() .
.
![]() 已知第6次考试该生的数学成绩达到132,请你估计第6次考试他的物理成绩大约是多少?
已知第6次考试该生的数学成绩达到132,请你估计第6次考试他的物理成绩大约是多少?
