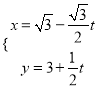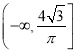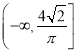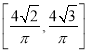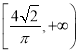题目内容
【题目】△ABC的内角A，B，C的对边分别是a，b，c，且2acosA＝bcosC＋ccosB.
(Ⅰ)求A的大小；
(Ⅱ)若a＝2，求b＋c的取值范围．
【答案】(Ⅰ) A＝
(Ⅱ) 
【解析】试题分析：（Ⅰ）通过正弦定理化简式子并分离出
利用两角和的正弦函数化简求值，再求出
的大小；
（Ⅱ）通过余弦定理以及基本不等式求出
的范围，再利用三角形三边的关系求出
的范围．
试题解析：(Ⅰ)∵2acosA＝bcosC＋ccosB ，
∴2sinAcosA＝sinBcosC＋sinCcosB ，
即cosA＝
＝
＝
，A∈(0，π)，∴A＝
；
(Ⅱ)由余弦定理知4＝b2＋c2－bc，
∴4≥2
2－
2＝
2，∴b＋c≤4，
又∵b＋c>a，∴b＋c>2，
综上，b＋c的取值范围为
.
练习册系列答案
阅读快车系列答案
相关题目
