题目内容

实数x，y满足不等式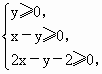

试求(1)w1＝x2＋y2的最小值；

(2)w2＝的取值范围．

答案：
解析：

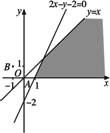
　　解：首先画出可行域，如图阴影部分．

　　(1)w1＝x2＋y2表示的是可行域内任意一点(x，y)到(0，0)点的距离的平方，由图可知，点A(x，y)到点O(0，0)的距离最小，点A的坐标是(1，0)．所以wmin＝12＋02＝1．

　　(2)w2＝表示的是可行域内任意一点(x，y)到B(－1，1)点连线的斜率，由图可知，点A(1，0)与B(－1，1)点连线的斜率最小，wmin＝＝－，wmax＝1(但取不到)，所以w2的取值范围是－≤w＜1．

　　思路解析：解本题的关键是搞清楚它们的几何意义，w1表示的是可行域内任意一点(x，y)到(0，0)点的距离的平方．w2表示的是可行域内任意一点(x，y)到(－1，－1)点连线的斜率．


练习册系列答案
相关题目
若实数x，y满足不等式组
x+3y-3≥0
2x-y-3≤0
x-my+1≥0
且x+y的最大值为9，则实数m=（　　）
A、-2B、-1C、1D、2
实数x，y满足不等式组
x-y+5≥0
x+y≥0
x≤3
，那么目标函数z=2x+4y的最小值是
 
．
实数x，y满足不等式组
|x|≤3
-3≤y≤2
x+y≥a
，若在平面直角坐标系中，由点（x，y）构成的区域的面积是22，则实数a的值为
 
．
（2012•汕头一模）实数x，y满足不等式组
2x-y≥0
x+y-2≥0
6x+3y≤18
，且z=ax+y（a＞0）取得最小值的最优解有无穷多个，则实数a的取值范围是（　　）
已知实数x，y满足不等式组
x-2y+1≥0
|x|-y-1≤0
，则x2+y2-6x+9的取值范围是
[2，16]
[2，16]
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网