题目内容
(2012•汕头一模)实数x,y满足不等式组
,且z=ax+y(a>0)取得最小值的最优解有无穷多个,则实数a的取值范围是( )
|
分析:先根据约束条件画出可行域,由z=ax+y,利用z的几何意义求最值,要使得取得最小值的最优解有无数个,只需直线z=ax+y与可行域的边界AC平行时,从而得到a值即可.
解答: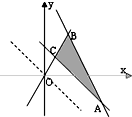 解:∵z=ax+y则y=-ax+z,z为直线y=-ax+z在y轴上的截距
解:∵z=ax+y则y=-ax+z,z为直线y=-ax+z在y轴上的截距
要使目标函数取得最小值的最优解有无穷多个,则截距最小时的最优解有无数个
∵a>0
把ax+y=z平移,使之与可行域中最左侧的点的边界AC重合即可,
∴-a=-1
∵a=1
故选B
 解:∵z=ax+y则y=-ax+z,z为直线y=-ax+z在y轴上的截距
解:∵z=ax+y则y=-ax+z,z为直线y=-ax+z在y轴上的截距要使目标函数取得最小值的最优解有无穷多个,则截距最小时的最优解有无数个
∵a>0
把ax+y=z平移,使之与可行域中最左侧的点的边界AC重合即可,
∴-a=-1
∵a=1
故选B
点评:本题主要考查了简单线性规划的应用、二元一次不等式(组)与平面区域等知识,解题的关键是明确z的几何意义,属于基础题.

练习册系列答案
 计算高手系列答案
计算高手系列答案
相关题目
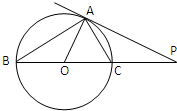 (2012•汕头一模)(几何证明选讲选做题)已知PA是⊙O的切线,切点为A,直线PO交⊙O于B、C两点,AC=2,∠PAB=120°,则⊙O的面积为
(2012•汕头一模)(几何证明选讲选做题)已知PA是⊙O的切线,切点为A,直线PO交⊙O于B、C两点,AC=2,∠PAB=120°,则⊙O的面积为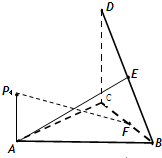 (2012•汕头一模)如图,直角△BCD所在的平面垂直于正△ABC所在的平面,PA⊥平面ABC,DC=BC=2PA,E为DB的中点.
(2012•汕头一模)如图,直角△BCD所在的平面垂直于正△ABC所在的平面,PA⊥平面ABC,DC=BC=2PA,E为DB的中点.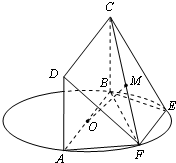 (2012•汕头一模)如图,AB为圆O的直径,点E、F在圆O上,AB∥EF,矩形ABCD所在的平面和圆O所在的平面互相垂直,且AB=2,AD=EF=1.
(2012•汕头一模)如图,AB为圆O的直径,点E、F在圆O上,AB∥EF,矩形ABCD所在的平面和圆O所在的平面互相垂直,且AB=2,AD=EF=1.