题目内容
12.现有A.B两枚均匀的骰子.用小莉掷A骰子朝上的数字为x、小明掷B骰子朝上的数字为y来确定点P(x,y),那么它们各掷一次所确定的点P落在已知抛物线y=-x2+4x上的概率为$\frac{1}{12}$.分析 由题意可知,P(x,y)共有6×6=36种等可能事件,找到确定的点P落在已知抛物线y=-x2+4x上的基本事件,根据概率公式计算即可.
解答  解:由题意可知,P(x,y)共有6×6=36种等可能事件,
解:由题意可知,P(x,y)共有6×6=36种等可能事件,
其中它们各掷一次所确定的点P落在已知抛物线y=-x2+4x上有(如图所示)(1,3),(2,4),(3,3)共3个基本事件,
故它们各掷一次所确定的点P落在已知抛物线y=-x2+4x上的概率为P=$\frac{3}{36}$=$\frac{1}{12}$,
故答案为:$\frac{1}{12}$.
点评 本题考查了古典概型的概率问题,关键是找到满足条件的基本事件的个数,利用数形结合的思想,比较容易找,属于基础题.

练习册系列答案
相关题目
13.已知△ABC的三条边长分别为3,4,5,如果把三角形的三边都增加相同的长度,则这个新三角形的形状为( )
| A. | 锐角三角形 | B. | 直角三角形 | ||
| C. | 钝角三角形 | D. | 由增加的长度决定 |
17.以平面直角坐标系的原点为极点,x轴的正半轴为极轴,建立极坐标系,两种坐标系中取相同的长度单位,已知圆C的参数方程是$\left\{\begin{array}{l}{x=cosθ-1}\\{y=sinθ-1}\end{array}\right.$(θ为参数),直线l的极坐标方程是ρcosθ+ρsinθ=2,则圆C上的点到直线l的最短距离为( )
| A. | 2$\sqrt{2}$-1 | B. | 2$\sqrt{2}$+1 | C. | $\sqrt{2}$ | D. | 2$\sqrt{2}$ |
2.在△ABC中,∠A=$\frac{π}{3}$,AB=2,且△ABC的面积为$\frac{{\sqrt{3}}}{2}$,则边AC的长为( )
| A. | 1 | B. | $\sqrt{3}$ | C. | 2 | D. | 1 |
 中,角
中,角 ,
, ,
,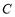 所对的边分别为
所对的边分别为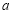 ,
, ,
, ,且满足
,且满足 .
. 的大小;
的大小; ,求
,求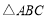 的周长的取值范围.
的周长的取值范围.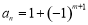 B.
B.
 D.
D.
 如图,圆O的直径AB=10,弦DE⊥AB于点H,BH=2.
如图,圆O的直径AB=10,弦DE⊥AB于点H,BH=2.