题目内容
16．已知函数f（x）=$\sqrt{\frac{x+1}{x-2}}$的定义域集合是A，函数g（x）=lg（x2-3x）的定义域是集合B．（1）求集合A，B；
（2）求A∪B，A∩B；
（3）求A∩（∁RB）．
分析 根据被开方数不小于0，真数大于0，解相应不等式，可得集合A，B，进而根据集合交集，并集，补集运算的定义，可得答案．
解答 解：（1）由$\frac{x+1}{x-2}≥0$得：x≤-1，或x＞2，
故A={x|x≤-1，或x＞2}，
由x2-3x＞0得：x＜0，或x＞3，
故B={x|x＜0，或x＞3}，
（2）A∪B={x|x＜0，或x＞2}，
A∩B={x|x≤-1，或x＞3}，
（3）∁RB={x|0≤x≤3}，
∴A∩（∁RB）={x|2＜x≤3}，
点评 本题考查的知识点是集合交集，并集，补集运算，难度不大，属于基础题．
练习册系列答案
相关题目
7．
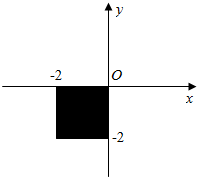用描述法表示下图所示阴影部分的点（包括边界上的点）的坐标的集合是（ ）
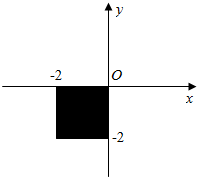用描述法表示下图所示阴影部分的点（包括边界上的点）的坐标的集合是（ ）| A． | {-2≤x≤0且-2≤y≤0} | B． | {（x，y）|-2≤x≤0且-2≤y≤0} | ||
| C． | {（x，y）|-2≤x≤0且-2≤y＜0} | D． | {（x，y）|-2≤x≤0或-2≤y≤0} |
8．已知二次函数y=f（x）的图象开口向下，且f（3-x）=f（3+x），则下列结论中，错误的是（ ）
| A． | f（0）＜f（7） | B． | f（6）＜f（4） | C． | f（2）＜f（$\sqrt{15}$） | D． | f（3+$\sqrt{2}$）=f（3-$\sqrt{2}$） |
5．函数的图象与x=1的交点最多有（ ）
| A． | 0个 | B． | 1个 | C． | 2个 | D． | 以上都不对 |
如图，在矩形ABCD中，已知AD=1.5，AB=a（a＞1.5），E，F，G，H分别是边AD，AB，BC，CD上的点，若AE=AF=CG=CH，问AE取何值时，四边形EFGH的面积最大，并求最大面积？