题目内容
4．抛物线y=$\frac{1}{4}$x2的焦点到准线的距离为（ ）| A． | 2 | B． | 1 | C． | $\frac{1}{2}$ | D． | $\frac{1}{8}$ |
分析 根据抛物线的方程求得抛物线的焦点坐标和准线的方程，进而利用点到直线的距离求得焦点到准线的距离．
解答 解：抛物线y=$\frac{1}{4}$x2可知焦点F（0，1），准线方程y=-1，
∴焦点到准线的距离是1+1=2．
故选：A．
点评 本题主要考查了抛物线的简单性质．考查了学生对抛物线标准方程的理解和运用，属基础题．
练习册系列答案
相关题目
5．已知$α∈（-\frac{π}{2}，0），\;β∈（0，\;\frac{π}{4}）$，$\frac{1}{2}-{sin^2}\frac{α}{2}=\frac{tanβ}{{1+{{tan}^2}β}}$，则有（ ）
| A． | $2β-α=\frac{π}{2}$ | B． | $2β+α=\frac{π}{2}$ | C． | $2β-α=-\frac{π}{2}$ | D． | $2β+α=-\frac{π}{2}$ |
12．为得到函数$y=sin（3x+\frac{π}{4}）$的图象，只要把函数$y=sin（x+\frac{π}{4}）$图象上所有的点（ ）
| A． | 横坐标缩短到原来的$\frac{1}{3}$倍，纵坐标不变 | |
| B． | 横坐标伸长到原来的3倍，纵坐标不变 | |
| C． | 纵坐标伸长到原来的3倍，横坐标不变 | |
| D． | 纵坐标缩短到原来的$\frac{1}{3}$倍，横坐标不变 |
16．已知抛物线C：y2=4x的焦点为F，准线为l，P是l上一点，Q是直线PF与C的一个交点，若$\overrightarrow{FP}=3\overrightarrow{FQ}$，则|QF|=（ ）
| A． | $\frac{8}{3}$ | B． | $\frac{4}{3}$ | C． | 2 | D． | 1 |
13．已知i是虚数单位，若（-1-2i）z=1-i则$\overline z$在复平面上所代表的点在（ ）
| A． | 第一象限 | B． | 第二象限 | C． | 第三象限 | D． | 第四象限 |
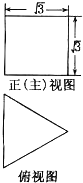一个底面为正三角形的直三棱柱的正视图和俯视图（单位：cm）如图所示，则它的外接球的表面积等于$\frac{25π}{3}$cm2．