题目内容
【题目】如图,A、B两点都在河的对岸(不可到达),为了测量A、B两点间的距离,选取一条基线CD,A、B、C、D在一平面内.测得:CD=200m,∠ADB=∠ACB=30°,∠CBD=60°,则AB=( ) 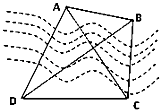
A.![]() m
m
B.200 ![]() m
m
C.100 ![]() m
m
D.数据不够,无法计算
【答案】A
【解析】解:如图所示,∵∠ADB=∠ACB=30°,∠CBD=60°,∴AC⊥BD.
设AC∩BD=O,则△AOD∽△BOC,∴OC=OD,△OCD为等腰直角三角形,
∴∠ODC=∠OCS=45°.
设OA=x,OB=y,则AD=2x,BC=2y,∴OD= ![]() x,OC=
x,OC= ![]() y.
y.
△COD中,由勾股定理可得3x2+3y2=40000,求得 x2+y2= ![]() ,
,
故AB= ![]() =
= ![]() .
.
故选:A.
【考点精析】关于本题考查的正弦定理的定义和余弦定理的定义,需要了解正弦定理:![]() ;余弦定理:
;余弦定理:![]() ;
;![]() ;
;![]() 才能得出正确答案.
才能得出正确答案.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
【题目】2016年中国(云南赛区)三对三篮球联赛在昆明市体育局的大力支持下,圆满顺利结束.组织方统计了来自![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 球队的男子的平均身高与本次比赛的平均得分,如下表所示:
球队的男子的平均身高与本次比赛的平均得分,如下表所示:
球队 |
|
|
|
|
|
平均身高 | 170 | 174 | 176 | 181 | 179 |
平均得分 | 62 | 64 | 66 | 70 | 68 |
(2)若![]() 队平均身高为
队平均身高为![]()
![]() ,根据(1)中所求得的回归方程,预测
,根据(1)中所求得的回归方程,预测![]() 队的平均得分.(精确到个位)
队的平均得分.(精确到个位)
注:回归方程![]() 中斜率和截距最小二乘估计公式分别为
中斜率和截距最小二乘估计公式分别为
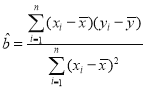 ,
,![]() .
.