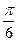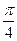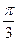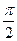题目内容
(本小题满分12分)
求与轴x轴相切,圆心在直线3x-y=0上,且被直线x-y=0截下的弦长2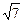 的圆的方程
的圆的方程
求与轴x轴相切,圆心在直线3x-y=0上,且被直线x-y=0截下的弦长2
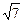 的圆的方程
的圆的方程圆方程为x2+y2-2x-6y+1=0,或x2+y2+2x+6y+1=0[
解:法一:设所求圆点方程是(x-a)2+(y-b)2=r2,
则圆心(a,b)到直线x-y=0的距离为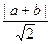 ,………………………….……3分
,………………………….……3分
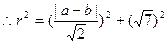 ,即2r2=(a-b)2+14 ①…………….………5分
,即2r2=(a-b)2+14 ①…………….………5分
由于所求圆与x轴相切,∴r2=b2 ②………………………..……7分
又所求圆心在直线3x-y=0上,∴3a-b="0 " ③ …………………………9分
联立①②③解得 a=1,b=3,r3=9,或a=-1,b=-3,r2=9,……………….11分
故所求圆方程为(x-1)2+(y-3)2=9或(x+1)2+(y+3)2=9.......... 12分
法二:设所求圆点方程为x2+y2+Dx+Ey+F=0
圆心为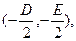 半径为
半径为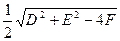
令y=0,得x2+Dx+F=0,由圆与x轴相切,得△=0,
即D2="4F " ①
 又圆心
又圆心 到直线x-y=0的距离为
到直线x-y=0的距离为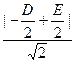 。
。
由已知得,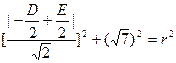
即(D-E)2+56=2(D2+E2-4F) ②
又圆心在直线3x-y=0上,∴3D-E="0 " ③
联立①②③得D=-2,E=-6,F=1或D=2,E=6,F=1
故所求圆方程为x2+y2-2x-6y+1=0,或x2+y2+2x+6y+1=0
则圆心(a,b)到直线x-y=0的距离为
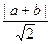 ,………………………….……3分
,………………………….……3分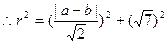 ,即2r2=(a-b)2+14 ①…………….………5分
,即2r2=(a-b)2+14 ①…………….………5分由于所求圆与x轴相切,∴r2=b2 ②………………………..……7分
又所求圆心在直线3x-y=0上,∴3a-b="0 " ③ …………………………9分
联立①②③解得 a=1,b=3,r3=9,或a=-1,b=-3,r2=9,……………….11分
故所求圆方程为(x-1)2+(y-3)2=9或(x+1)2+(y+3)2=9.......... 12分
法二:设所求圆点方程为x2+y2+Dx+Ey+F=0
圆心为
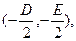 半径为
半径为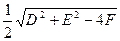
令y=0,得x2+Dx+F=0,由圆与x轴相切,得△=0,
即D2="4F " ①
 又圆心
又圆心 到直线x-y=0的距离为
到直线x-y=0的距离为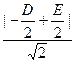 。
。由已知得,
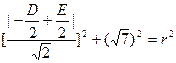
即(D-E)2+56=2(D2+E2-4F) ②
又圆心在直线3x-y=0上,∴3D-E="0 " ③
联立①②③得D=-2,E=-6,F=1或D=2,E=6,F=1
故所求圆方程为x2+y2-2x-6y+1=0,或x2+y2+2x+6y+1=0

练习册系列答案
相关题目
 与圆
与圆 相交于
相交于 两点,
两点, 为坐标原点,
为坐标原点, 的面积为
的面积为 .
.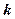 的函数
的函数 ,并求出其定义域;
,并求出其定义域;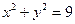 与直线
与直线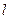 交于
交于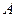 、
、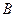 两点,若线段
两点,若线段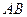 的中点
的中点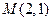
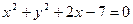 内一点
内一点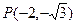 ,过点
,过点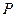 的直线
的直线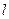 的倾斜角为
的倾斜角为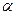 ,直线
,直线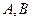 两点,
两点,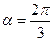 时,求弦
时,求弦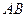 的长;
的长;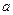 x-y+3=0与圆
x-y+3=0与圆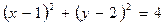 相交于A,B两点,且弦AB的长为
相交于A,B两点,且弦AB的长为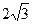 ,则
,则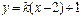 与曲线
与曲线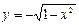 有两个不同的交点,则k 的取值范围是 ( )
有两个不同的交点,则k 的取值范围是 ( )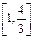
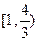
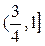
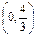
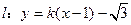 与圆
与圆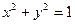 相切,则直线
相切,则直线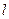 的倾斜角为 ( )
的倾斜角为 ( )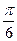
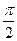
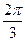
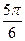
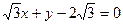 截圆
截圆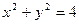 得到的劣弧所对的圆心角为 ( )
得到的劣弧所对的圆心角为 ( )