题目内容
【题目】在平面直角坐标系![]() 中,已知直线
中,已知直线![]() ∶
∶![]() 和圆
和圆![]() ∶
∶![]() ,
,![]() 是直线
是直线![]() 上一点,过点
上一点,过点![]() 作圆
作圆![]() 的两条切线,切点分别为
的两条切线,切点分别为![]() .
.
(1)若![]() ,求点
,求点![]() 坐标;
坐标;
(2)若圆![]() 上存在点
上存在点![]() ,使得
,使得![]() ,求点
,求点![]() 的横坐标的取值范围;
的横坐标的取值范围;
(3)设线段![]() 的中点为
的中点为![]() ,
,![]() 与
与![]() 轴的交点为
轴的交点为![]() ,求线段
,求线段![]() 长的最大值.
长的最大值.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)先求出![]() 到圆心的距离为
到圆心的距离为![]() ,设
,设![]() ,解方程
,解方程![]() 即得解;(2)设
即得解;(2)设![]() ,若圆
,若圆![]() 上存在点
上存在点![]() ,使得
,使得![]() ,分析得到
,分析得到![]() ,即
,即![]() ,解不等式得解;(3)设
,解不等式得解;(3)设![]() ,可得
,可得![]() 所在直线方程:
所在直线方程:![]() ,
,![]() 点的轨迹为:
点的轨迹为: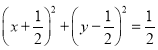 ,根据
,根据![]() 求出最大值得解.
求出最大值得解.
(1)若![]() ,则四边形
,则四边形![]() 为正方形,
为正方形,
则![]() 到圆心的距离为
到圆心的距离为![]() ,
,
∵![]() 在直线
在直线![]() 上,设
上,设![]()
故![]() ,解得
,解得![]() ,故
,故![]() ;
;
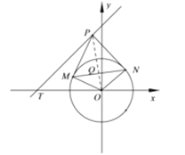
(2)设![]() ,若圆
,若圆![]() 上存在点
上存在点![]() ,使得
,使得![]() ,
,
过![]() 作圆的切线
作圆的切线![]() ,
,![]() ,∴
,∴![]() ,∴
,∴![]() ,
,
在直角三角形![]() 中,∵
中,∵![]() ,
,
∴![]() ,即
,即![]() ,∴
,∴![]() ,
,
∴![]() ,解得
,解得![]() ,
,
∴点![]() 横坐标的取值范围为:
横坐标的取值范围为:![]() ;
;
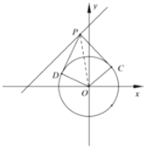
(3)设![]() ,则以
,则以![]() 为直径的圆的方程为
为直径的圆的方程为
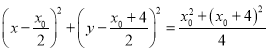
化简得![]() ,与
,与![]() 联立,
联立,
可得![]() 所在直线方程:
所在直线方程:![]() ,
,
联立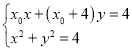 ,得
,得![]() ,
,
∴![]() 的坐标为
的坐标为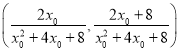 ,
,
可得![]() 点的轨迹为:
点的轨迹为: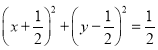 ,
,
圆心![]() ,半径
,半径![]() .其中原点
.其中原点![]() 为极限点(也可以去掉).
为极限点(也可以去掉).
由题意可知![]() ,∴
,∴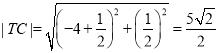 .
.
∴![]() .
.
∴线段![]() 的最大值为
的最大值为![]() .
.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目