Question

【题目】已知抛物线y＝x2和点P（0，1），若过某点C可作抛物线的两条切线，切点分别是A，B，且满足，则△ABC的面积为_____．

Answer 1

【答案】．

【解析】

由可得,则有直线恒过定点,设直线方程与抛物线方程联立,即可解得弦的长,对抛物线方程求导,求得切线方程的斜率,可求得切线方程,进而解得点坐标,利用点到直线的距离公式,三角形面积公式,即可解得所求.

∵，则3（2（），

∴2，

故直线AB过点P，且AP＝2PB．

故设直线AB：y＝kx+1，A（x1，y1），b（x2，y2）

联立可得x2﹣kx﹣1＝0，则x1x2＝﹣1，x1+x2＝k．

由AP＝2PB．可得x1+2x2＝0

可得k，AB

由导数y′＝2x，

可得过A，B的切线分别为y+y1＝2x1x，y+y2＝2x2x，

联立切线方程可得C（，﹣1）

C到y＝kx+1的距离d．

则△ABC的面积为S．

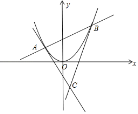
故答案为: .