题目内容
已知函数 在区间(0,1)内任取两个实数p,q,且p≠q,不等式
在区间(0,1)内任取两个实数p,q,且p≠q,不等式 恒成立,则实数
恒成立,则实数 的取值范围为( )
的取值范围为( )
 在区间(0,1)内任取两个实数p,q,且p≠q,不等式
在区间(0,1)内任取两个实数p,q,且p≠q,不等式 恒成立,则实数
恒成立,则实数 的取值范围为( )
的取值范围为( )A. | B. | C. | D. |
A
试题分析:由已知得,
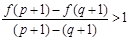 ,且
,且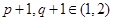 ,等价于函数
,等价于函数 在区间
在区间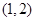 上任意两点连线的割线斜率大于1,等价于函数在区间
上任意两点连线的割线斜率大于1,等价于函数在区间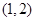 的切线斜率大于1恒成立.
的切线斜率大于1恒成立.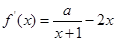 ,即
,即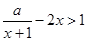 恒成立,变形为
恒成立,变形为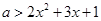 ,因为
,因为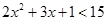 ,故
,故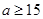 .
.
练习册系列答案
相关题目
题目内容
 在区间(0,1)内任取两个实数p,q,且p≠q,不等式
在区间(0,1)内任取两个实数p,q,且p≠q,不等式 恒成立,则实数
恒成立,则实数 的取值范围为( )
的取值范围为( )A. | B. | C. | D. |
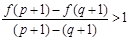 ,且
,且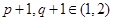 ,等价于函数
,等价于函数 在区间
在区间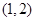 上任意两点连线的割线斜率大于1,等价于函数在区间
上任意两点连线的割线斜率大于1,等价于函数在区间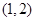 的切线斜率大于1恒成立.
的切线斜率大于1恒成立.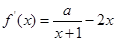 ,即
,即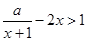 恒成立,变形为
恒成立,变形为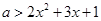 ,因为
,因为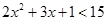 ,故
,故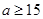 .
.