题目内容
已知函数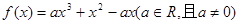 .如果存在实数
.如果存在实数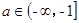 ,使函数
,使函数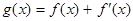 ,
,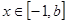
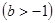 在
在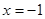 处取得最小值,则实数
处取得最小值,则实数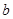 的最大值为 .
的最大值为 .
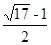
解析试题分析:依题意,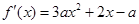 ,
,
令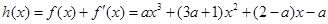 ,
,
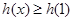 在区间
在区间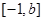 上恒成立,
上恒成立,
即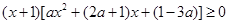 ①
①
当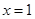 时不等式①成立,
时不等式①成立,
当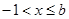 时,不等式①可化为
时,不等式①可化为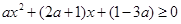 ②
②
令 ,
,
由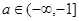 知其图象是开口向下的抛物线,
知其图象是开口向下的抛物线,
故它在闭区间上的最小值必在端点处取得,
又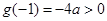 ,则不等式②成立的充要条件是
,则不等式②成立的充要条件是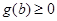 ,
,
整理得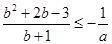 在
在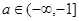 上有解,即
上有解,即 ,
,
解得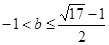 ,故实数
,故实数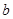 的最大值为
的最大值为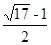 .
.
考点:函数的极值、最值,不等式的解法,恒成立.

练习册系列答案
相关题目
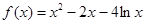 ,则
,则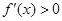 的解集为 。
的解集为 。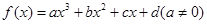 的对称中心为
的对称中心为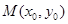 ,记函数
,记函数 的导函数为
的导函数为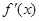 ,
,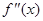 ,则有
,则有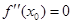 .若函数
.若函数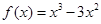 ,则可求得
,则可求得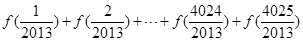 _________.
_________. 在点
在点 处的切线方程为 ___________________
处的切线方程为 ___________________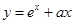 有大于零的极值点,则
有大于零的极值点,则 的取值范围是_________.
的取值范围是_________.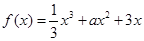 在(0, 1)上不是单调函数,则实数
在(0, 1)上不是单调函数,则实数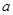 的取值范围为 _____.
的取值范围为 _____.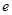 是自然对数的底数,若函数
是自然对数的底数,若函数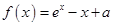 的图象始终在
的图象始终在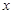 轴的上方,则实数
轴的上方,则实数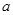 的取值范围 .
的取值范围 .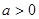 ,则函数
,则函数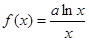 的单调递增区间是________.
的单调递增区间是________.