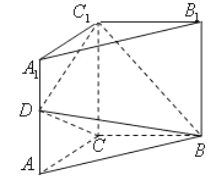
题目内容
【题目】如图，矩形ABCD中，
，
，F分别在线段BC和AD上，
，将矩形ABEF沿EF折起
记折起后的矩形为MNEF，且平面
平面ECDF．
Ⅰ
求证：
平面MFD；
Ⅱ若
，求证：
；
Ⅲ求四面体NFEC体积的最大值．
【答案】（1）见解析（2）见解析（3）
【解析】
试题分析：（1）证明：因为四边形MNEF，EFDC都是矩形，所以MN∥EF∥CD，MN=EF=CD．
所以四边形MNCD是平行四边形，所以NC∥MD，因为NC平面MFD，所以NC∥平面MFD． 4分
（2）证明：连接ED，设ED∩FC=O．因为平面MNEF⊥平面ECDF，且NE⊥EF，所以NE⊥平面ECDF， 5分
所以FC⊥NE．又EC=CD，所以四边形ECDF为正方形，所以 FC⊥ED．所以FC⊥平面NED，
所以ND⊥FC． 8分
（3）解：设NE=
，则EC=4-，其中0＜x＜4．由（1）得NE⊥平面FEC，所以四面体NFEC的体积为
，所以
.
当且仅当
，即x=2时，四面体NFEC的体积有最大值2．
练习册系列答案
百年学典课时学练测系列答案
仁爱英语同步练习册系列答案
相关题目
【题目】国家射击队的某队员射击一次，命中7~10环的概率如表所示：
命中环数 | 10环 | 9环 | 8环 | 7环 |
概率 | 0.32 | 0.28 | 0.18 | 0.12 |
求该射击队员射击一次 求:
（1）射中9环或10环的概率；
（2）至少命中8环的概率；（3）命中不足8环的概率。
