题目内容
1.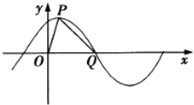 已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,0<φ<$\frac{π}{2}$)的部分图象如图所示,P是图象的最高点,Q为图象与x轴的交点,O为坐标原点,若OQ=4,OP=$\sqrt{5}$,PQ=$\sqrt{13}$.
已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,0<φ<$\frac{π}{2}$)的部分图象如图所示,P是图象的最高点,Q为图象与x轴的交点,O为坐标原点,若OQ=4,OP=$\sqrt{5}$,PQ=$\sqrt{13}$.(1)求函数y=f(x)的解析式;
(2)将函数y=f(x)的图象向右平移2个单位后得到函数y=g(x)的图象,当x∈[0,3]时,求函数h(x)=f(x)•g(x)的值域.
分析 (1)从给出的三角函数图象中给出三个线段信息,从中可以求出图象最高点的坐标,$\frac{T}{4}$的长度,由此推理出三角函数的解析式;
(2)由题意先求出g(x),h(x)的函数解析式,由x的范围求出$\frac{π}{3}$x-$\frac{π}{6}$的范围,同时结合三角函数的图象进行分析,即可求出其函数值域.
解答 解:(1)由条件知cos∠POQ=$\frac{{4}^{2}+(\sqrt{5})^{2}-(\sqrt{13})^{2}}{2×4×\sqrt{5}}$=$\frac{\sqrt{5}}{5}$,所以P(1,2). (2分)
由此可得振幅A=2,周期T=4×(4-1)=12,又$\frac{2π}{ω}$=12,则ω=$\frac{π}{6}$.
将点P(1,2)代入f(x)=2sin($\frac{π}{6}$x+φ),得sin($\frac{π}{6}$x+φ)=1,
因为0<φ<$\frac{π}{2}$,所以φ=$\frac{π}{3}$,于是f(x)=2sin($\frac{π}{6}$x+$\frac{π}{3}$). (6分)
(2)由题意可得g(x)=2sin[$\frac{π}{6}$(x-2)+$\frac{π}{3}$]=2sin$\frac{π}{6}$x.
所以h(x)=f(x)•g(x)=4sin($\frac{π}{6}$x+$\frac{π}{3}$)•sin$\frac{π}{6}$x=2sin2$\frac{π}{6}$x+2$\sqrt{3}$sin$\frac{π}{6}$x•cos$\frac{π}{6}$x=1-cos$\frac{π}{3}$x+$\sqrt{3}$sin$\frac{π}{3}$x=1+2sin($\frac{π}{3}$x-$\frac{π}{6}$). (9分)
当x∈[0,3]时,$\frac{π}{3}$x-$\frac{π}{6}$∈[-$\frac{π}{6}$,$\frac{5π}{6}$],所以sin($\frac{π}{3}$x-$\frac{π}{6}$)∈[-$\frac{1}{2}$,1],即1+2sin($\frac{π}{3}$x-$\frac{π}{6}$)∈[0,3].
于是函数h(x)的值域为[0,3]. (12分)
点评 本题主要考查了三角函数图象的平移、三角函数的恒等变换及三角函数的值域等知识,考查了求解三角函数的值域,关注自变量x的取值范围是解题的关键,属于中档题.

 名校课堂系列答案
名校课堂系列答案| A. | 若m∥α,n∥α,m,n共面,则m∥n | B. | 若m?α,n∥α,m,n共面,则m∥n | ||
| C. | 若m?α,n?a,m,n异面,则m∥n | D. | 若m?α,n?α,m,n异面,则m与n相交 |
 如图,在五面体ABCDEF中,四边形 ABCD是边长为4的正方形,EF∥AD,平面ADEF⊥平面ABCD,且BC=2EF,AE=AF,点G是EF的中点.
如图,在五面体ABCDEF中,四边形 ABCD是边长为4的正方形,EF∥AD,平面ADEF⊥平面ABCD,且BC=2EF,AE=AF,点G是EF的中点.